Решение. и число a = 4. Вычислить матрицы: С = А + В,D = A – B, M = aА

Пример 1.1.3.

Даны матрицы

,

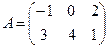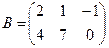
и число a = 4. Вычислить матрицы: С = А + В, D = A – B, M = aА

а) ;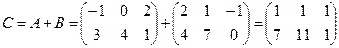

б) ;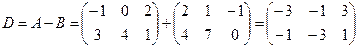

в) .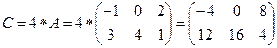

Умножение матриц А и В, т. е. получение произведения этих матриц С = АВ, возможно лишь в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Такие матрицы называются согласованными.

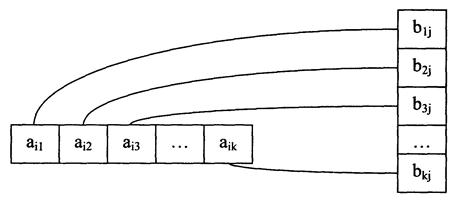
Рис. 1.1.1

Произведением двух согласованных матриц 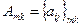и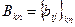
называется такая третья матрица 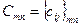, для которой каждый элемент
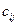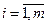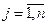, , ,п вычисляется по формуле (рис. 1.1.1)

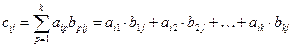(1.1.2)

Пример 1.1.4. Вычислить произведение матриц

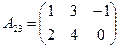и .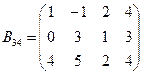

Можно ли получить произведение ВА?

Решение. Число столбцов матрицы А(3) равно числу строк матрицы В(3). Поэтому произведение АВ = С определено. Матрица С имеет размер­ность 2x4, а ее элементы вычисляются по формуле (1.1.2)

,

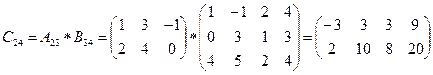где ;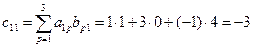

;

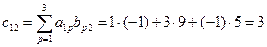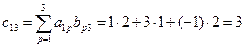и т.д.

Произведение ВА не определено, т. к. число столбцов матрицы В(4) не равно числу строк матрицы А(2).

Определителем (1.1.1) матрицы второго порядка называется число

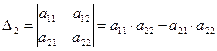
Определителем матрицы третьего порядка называется число

.

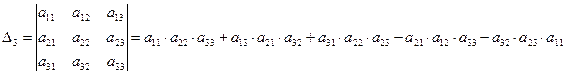Студенту следует обратить внимание на правила треугольника и Силь­вестра вычисления определителей третьего порядка.

Пример 1.1.5. Вычислить определитель

.

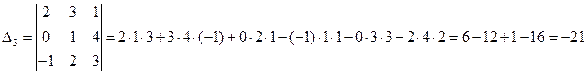Минором 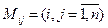элемента a_ij определителя называется опреде­литель, который получается из данного определителя вычеркиванием строки и столбца, на пересечении которых находится элемент a_ij.

Алгебраическим дополнением 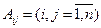элемента a_ij определителя называется его минор, взятый со знаком (-l)^i+j, т. е.

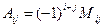. (1.1.3)

Пример 1.1.6. Записать миноры и алгебраические дополнения элемен­тов определителя примера 1.1.5.

; ; ;

; ; ;

; ; ;

; ; ;

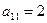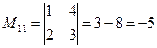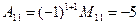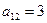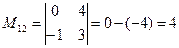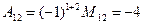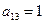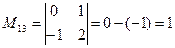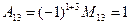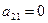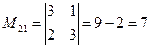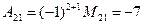Замечание. Определители матриц n -го порядка (n = 1, 2...) короче на­зывают определителями n -го порядка.

Свойства определителей:

1) определитель не изменится, если транспонировать матрицу определителя;

2) при перестановке двух соседних строк (столбцов) определитель меняет знак;

3) определитель с двумя одинаковыми строками (столбцами) равен 0;

4) общий множитель для элементов строки (столбца) можно вынести за знак
определителя;

5) определитель равен 0, если все элементы строки (столбца) равны 0;

6) определитель не изменится, если к элементам строки (столбца) прибавить
элементы другой строки (столбца), предварительно умножив их на один и
тот же множитель;

7) определитель равен сумме произведений элементов любой строки (столб­ца) на их алгебраические дополнения, например:

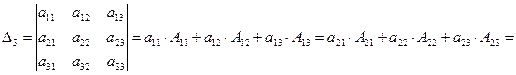(1.1.4)

.

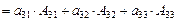Пример 1.1.7. Вычислить определитель примера 1.1.5, используя свой­ство семи определителей (разложение произвести по элементам первого столбца).

.

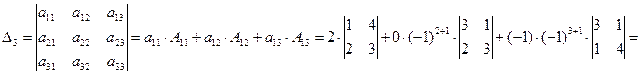
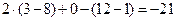По аналогии с формулой (1.1.4) вводятся определители n -го порядка

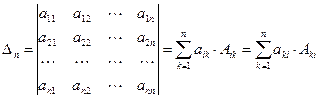
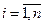. (1.1.5)

Пример 1.1.8. Используя свойства 1-7 определителей, вычислить оп­ределитель четвертого порядка

используя свойство 2, переставим местами первую и вторую строки

используя свойство 2, переставим местами первую и вторую строки

.

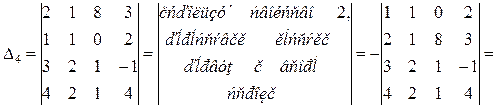
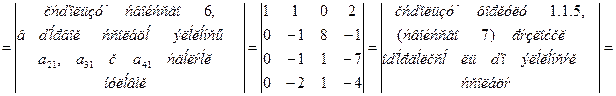
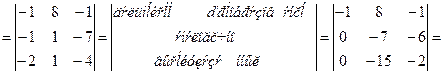
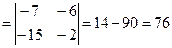Матрицей, обратной к матрице А, называется квадратная матрица А^-1, такая, что А^-1А = Е.

Если матрица А невырожденная (det А ≠ 0), то обратная матрица А^-1 находится по формуле

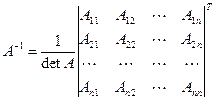, (1.1.6)

где 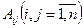‑ алгебраические дополнения элементов а_ij (1.1.3).

Пример 1.1.9. Найти матрицу, обратную к данной матрице

.

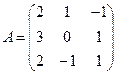Вычислим определитель матрицы А:

.

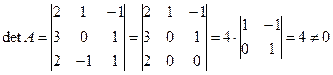По формуле (1.1.6) находим (вычисление алгебраических дополнений элементов матрицы А рассмотрено в примере 1.1.6):

.

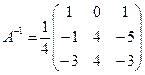Проверка:

.

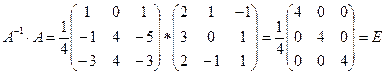Студентам рекомендуется провести вычисление обратной матрицы ме­тодом элементарных преобразований.

Рангом матрицы А размерности m × n называется наибольший из по­рядков ее миноров, отличных от нуля. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка большего, чем r, равен 0. Ранг матрицы обозначается r(А).

Свойства ранга матрицы А размерности m x п:

1) 0 <r<min(m, n);

2) r = 0 тогда и только тогда, когда матрица нулевая;

3) для квадратной матрицы n -го порядка r = n тогда и только тогда, когда матрица невырожденная;

4) ранг транспонированной матрицы равен рангу исходной матрицы;

5) ранг матрицы не изменится, если вычеркнуть (дописать) нулевую строку (столбец);

6) ранг матрицы не изменится, если к элементам строки матрицы прибавить элементы другой строки матрицы, предварительно умноженные на неко­торое число;

7) ранг матрицы не изменится, если переставить любые строки (столбцы) матрицы.

Пример 1.1.10. Найти ранг матрицы А.

.

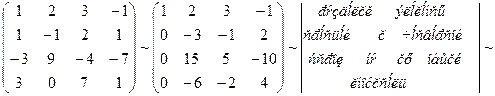
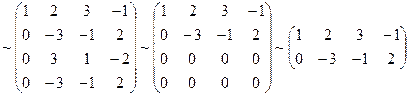rgA = 2, т. к. имеется отличный от нуля определитель второго порядка, например .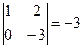

Студент должен уметь решать системы линейных алгебраических уравнений (в дальнейшем СЛАУ):

1) по формулам Крамера и матричным методом (в случае, когда матрица А
системы невырожденная);

2) произвольные СЛАУ с использованием теоремы Кронекера - Капелли ме­тодом Гаусса.

Рассмотрим примеры на применение этих двух методов. 1) Предположим, что СЛАУ имеет невырожденную матрицу порядка n.

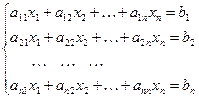
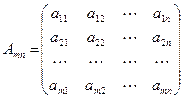, det A ≠ 0, , ,

, .

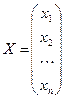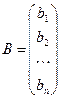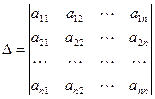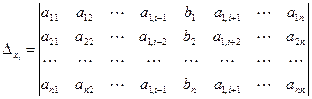Правило Крамера. Если главный определитель СЛАУ отличен от нуля (∆ ≠ 0), то СЛАУ имеет единственное решение, которое находится по формуле

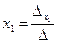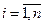, (1.1.7)

Матричный метод. Если матрица СЛАУ невырожденная, то решение СЛАУ может быть найдено по формуле

Х = А^-1В, (1.1.8)

где матрица А^-1 вычисляется по формуле (1.1.6) либо методом элементарных преобразований.

Пример 1.1.11. Решить СЛАУ

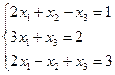
а) по формулам Крамера;

б) методом обратной матрицы.

Решение. Запишем матрицу системы А, матрицу-столбец неизвестных x и матрицу-столбец свободных членов В:

, , .

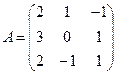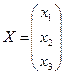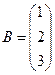а) ,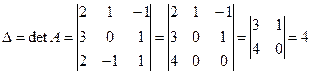

,

,

,

; ; ;

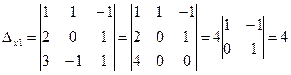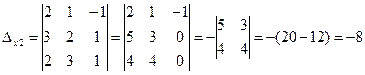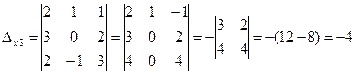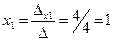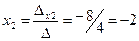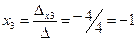б) воспользуемся формулой X = А^-1В, где матрица А^-1 вычислена в примере 1.1.9:

.

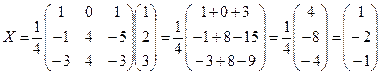Таким образом, 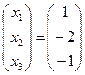, или .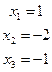

2) Предположим, что матрица СЛАУ имеет размерность m x п. В этом слу­чае СЛАУ имеет вид

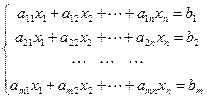
Запишем расширенную матрицу системы :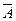

.

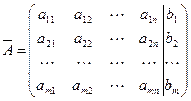Теорема Кронекера - Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу матрицы системы.

Для решения произвольных СЛАУ применяется метод Гаусса. Сущ­ность метода состоит в том, что расширенная матрица СЛАУ приводится к ступенчатому виду.

Пример 1.1.12. Решить систему

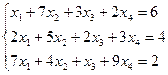
В этой системе m = 3 - количество уравнений; n = 4 - количество неиз­вестных.

Решение. Запишем расширенную матрицу системы А и преобразуем ее к ступенчатому виду:

.

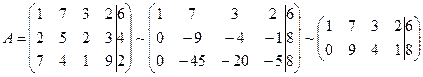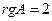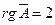, . реме Кронекера - Капелли СЛАУ совместна. Укороченная СЛАУ имеет вид

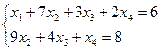
В качестве базисных неизвестных выберем неизвестные x₁ и х₂, а неиз­вестные х₃, х₄ примем за свободные, полагая х₃ = С₁, х₄ = С₁. Тогда СЛАУ может быть записана в виде

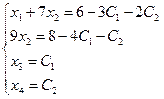
Отсюда находим ,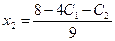

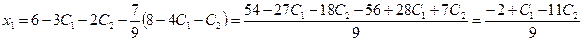
и окончательно получим

.

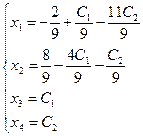
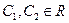Пример 1.1.13. Решить систему

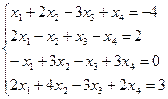
Дата добавления: 2014-11-20