Прямая линия на плоскости

Взаимное расположение прямой и плоскости

Пусть плоскость задана уравнением (1.3.2), а прямая - уравнениями (1.3.6) либо (1.3.7), тогда 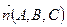‑ нормаль к плоскости, 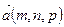‑ направляющий вектор прямой.

Рис. 1.3.1 Рис. 1.3.2

1. Условие перпендикулярности прямой и плоскости:

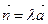, или 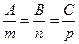. (1.3.21)

2. Условие параллельности прямой и плоскости

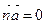, или . (1.3.22)

3. Угол между прямой и плоскостью (рис. 1.3.1):

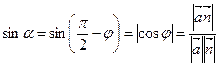. (1.3.23)

4. Координаты точки пересечения прямой и плоскости находятся из системы уравнений (1.3.2) и (1.3.7), а именно:

. (1.3.24)

5. Проекция точки M₁(x₁,y₁,z₁) на прямую (рис. 1.3.2). Координаты точки Р определяются из системы

(1.3.25)

где плоскость 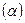проведена через точку M₁ перпендикулярно прямой L.

Уравнение прямой линии на плоскости может быть получено из канонических уравнений прямой в пространстве (1.3.6), если положить z₀=0 и р=0, то

, или (1.3.26)

В зависимости от условий задачи уравнение прямой на плоскости может быть записано в виде:

а) у=кх+b (1.3.27)

– уравнение прямой с угловым коэффициентом;

б) a х+by+c=0 (1.3.28)

– общее уравнение прямой;

в) у=у₀+к(х-х₀) (1.3.29)

- уравнение прямой, проходящей через точку М₀(х₀,у₀) и имеющей заданный угловой коэффициент k;

г) (1.3.30)

- уравнение прямой, проходящей через две заданные точки. Угол между двумя прямыми у=k₁x+b₁ и у=k₂х+b₂ определяется по формуле

. (1.3.31)

Условия параллельности и перпендикулярности прямых, соответственно, имеют вид

k₁=k₂ (1.3.32)

. (1.3.33)

Пример 1.3.10. Треугольник задан координатами вершин A₁(1,2), А₂(4,0), А₃(6,3). Написать уравнения:

1) стороны А₁А₃;

2) медианы, проведенной из вершины А₂;

3) высоты, проведенной из вершины А₂.

Решение. 1) Воспользуемся уравнением (1.3.30):

; ; ;

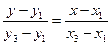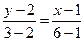‑ уравнение стороны А₁А₃.

2) пусть точка К ‑ точка пересечения медианы треугольника, проведенной из вершины А₂, со стороной А₁А₃. Точка K - середина отрезка А₁А₃. Поэтому ее координаты равны полусумме координат концов отрезка, а именно: . Воспользуемся уравнением (1.3.30):

; ; ;

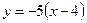; — уравнение медианы A₂К.

3) Высота, проведенная из вершины А₂, перпендикулярна стороне А₁А₃, поэтому угловой коэффициент k: определяется из условия (1.3.33):

.

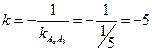Воспользуемся уравнением (1.3.29): у=у₂+к(х-х₂); у=0-5(х-4); у=-5х+20, т. е. высота треугольника А₁А₂А₃, проведенная из вершины А₂, совпадает с медианой, проведенной из этой же вершины.

Дата добавления: 2014-11-20