Уравнение плоскостей

Уравнения нецентральных поверхностей второго порядка

Уравнения центральных поверхностей второго порядка

1. 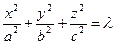, (1.6.6)

если – точка; – эллипс; 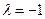– мнимый эллипс.

2. , (1.6.7)

если – однополостной гиперболоид; 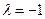– двуполостной гиперболоид; – эллиптический конус.

1. , (1.6.8)

если – эллиптический параболоид; 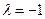– гиперболический параболоид.

2. Цилиндрические поверхности:

а) , (1.6.9)

если – эллиптический цилиндр; 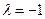– гиперболический цилиндр.

б) 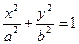, (1.6.10)

– мнимый эллиптический цилиндр (уравнению не удовлетворяет ни одна точка);

в) 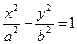, (1.6.11)

– пара плоскостей;

г) , , 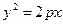(1.6.12)

и т. д. - параболические цилиндры.

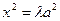, , если – пара параллельных плоскостей; 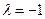‑ мнимые плоскости (уравнению не удовлетворяет ни одна точка пространства); – пара совпадающих плоскостей.

Пример 1.6.1. Записать каноническое уравнение кривой второго порядка 3х²+4ху–4х–8у=0 (сравните с решением примера 1.4.1 темы 1.4).

Квадратичная форма, содержащаяся среди слагаемых левой части уравнения, имеет вид 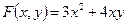, а ее матрица — , а₁₁=3, а₂₂=0, а₁₂=а₂₁=2.

Вычислим собственные числа и собственные векторы матрицы A (см. тему 1.5).

Пусть собственные векторы , где 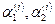— координаты. Система (1.5.5) для нахождения собственных векторов имеет вид

(1.6.14)

Найдем собственные числа Л, решив характеристическое уравнение (1.5.6).

; . Подставим первое собственное число в систему (1.6.14):

, , , .

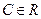Откуда и соответствующий единичный вектор имеет вид

Подставим второе собственное число в систему (1.6.14):

, , , , , .

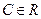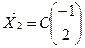Перейдем в двумерное пространство R₂ к новому базису, составленному из собственных векторов матрицы A и . При этом матрица квадратичной формы В в новом базисе будет иметь вид (см. формулу 1.5.3)

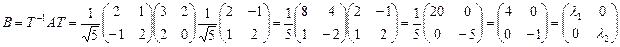
где матрица Т составлена из координат собственных векторов, записанных в столбцы. Связь между старыми координатами х,у (в базисе 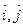) и новыми координатами x₁,y₁ (в новом базисе) реализуется по формуле

, или ,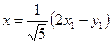

, а квадратичная форма в новом базисе имеет вид (аналогично формуле (1.6.3)) (случай двух переменных) .

Запишем уравнение кривой второго порядка в новых координатах, приведем подобные:

,

.

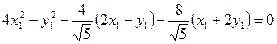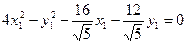Уравнение совпало с уравнением, полученным в примере 1.4.1 темы 1.4, и поэтому дальнейшие преобразования идентичны.

Ответ: – сопряженная гипербола с полуосями а=1, b=2.

Пример 1.6.2. Записать каноническое уравнение поверхности второго порядка 11х² + 4ху + 2у² – 16xz + 20yz + 5z² + 6x + 12y – 6 = 0.

Решение. Запишем квадратичную форму, входящую в состав левой части уравнения F(x,y,z) = 11х² + 4ху + 2у² – 16xz + 20yz + 5z².

Матрица этой квадратичной формы .

Собственные числа этой матрицы , , 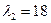, и единичные собственные векторы 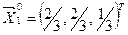, , , найдены в примере 1.5.4 (см. тему 1.5). Связь между координатами x, y, z в старом базисе 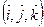и координатами x₁, y₁, z₁ в новом базисе 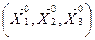имеет вид

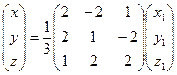, или ,

Вышезаписанная матрица, как в примере 1.6.1, образована из координат собственных векторов, записанных в столбцы. Матрица квадратичной формы В в новом базисе — диагональная , а сама квадратичная форма имеет вид .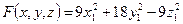

Запишем уравнение поверхности второго порядка в новых координатах, приведем подобные члены и выделим полные квадраты:

;

;

;

;

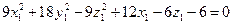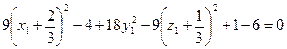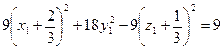
Перейдем к новым координатам (параллельный перенос): 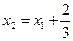; ; ; 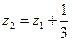или .

Полученное уравнение является каноническим уравнением однополостного гиперболоида (1.6.7) с параметрами .

После изучения материала, содержащегося в разделе 1, студент должен выполнить контрольную работу № 1.

Дата добавления: 2014-11-20