Решение. 1. Вектор имеет координаты:

1. Вектор 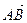имеет координаты: 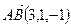. Поэтому его длина равна 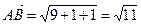(ед.)

2. Угол 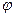между векторам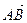и и 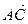определяется по формуле (1.2.3). Вычислим длину вектора :

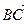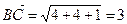(ед.).

.

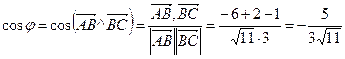Скалярное произведение вычислялось по формуле (1.2:5):

.

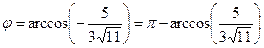3. Площадь треугольника ABC вычислена в примере 1.2.9.

4. Объем пирамиды ABCD вычислен в примере 1.2.10.

5. Длина высоты DH пирамиды, проведенной из вершины D к грани ABC, также вычислена в примере 1.2.10.

6. Уравнение прямой АВ будем искать в виде (1.3.8), т. к. заданы две точки этой прямой А и В.

.

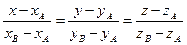Подставляя в последнее уравнение координаты точек А и В, получим

.

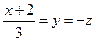7. Уравнение плоскости ABC можно записать в виде (1.3.4), т. к. заданы координаты трех точек А, В, С

;

.

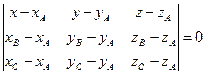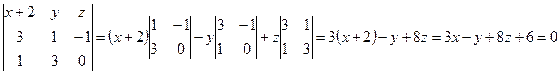Уравнение плоскости ABC:3x – y – 8z + 6 = 0.

8. Уравнение высоты пирамиды DH ищем в виде (1.3.6)

.

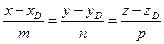Координаты точки D известны, а направляющий вектор прямой коллинеарен вектору нормали к плоскости ABC. Вектор нормали к плоскости ABC 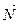имеет координаты 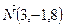(см. п. 7 данной задачи). Поэтому уравнение прямой DH имеет вид

.

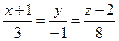9. Уравнение медианы AM ищем в виде (1.3.8):

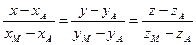
Точка М — середина отрезка ВС и имеет координаты:

; ;

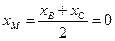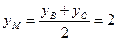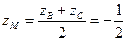
Таким образом, уравнение медианы AM имеет вид

.

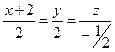10. Уравнение высоты АК ищем в виде (1.3.6):

.

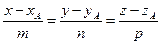Направляющий вектор прямой 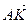вектор 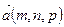перпендикулярен вектору 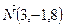— нормали к плоскости ABC и вектору 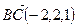(рис. Д.1.1). Поэтому вектор а может быть вычислен по формуле (1.2.10)

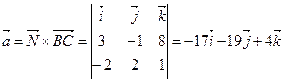
Уравнение высоты АК имеет вид .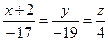

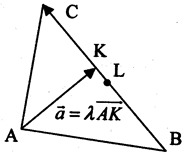
Рис. Д. 1.1

11. Точка L -точка пересечения биссектрисы AL со стороной ВС – делит отрезок ВС на части, длины которых пропорциональны длинам прилежащих сторон, т. е.

; ; .

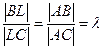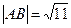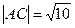Таким образом, 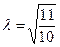и .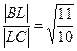

По формулам деления отрезка в данном отношении находим координаты точки L:

;

;

.

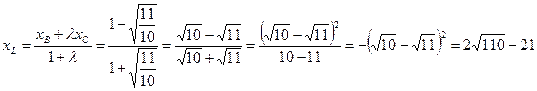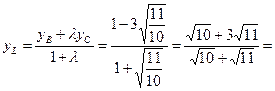
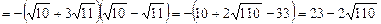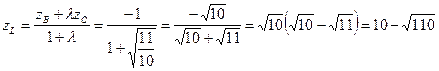Уравнение биссектрисы AL ищем в виде (1.3.8)

.

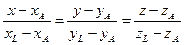Подставляя в последнее уравнение координаты точек А и L, получим

.

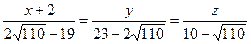Задача № 3. Составить уравнение плоскости, проходящей через точку М(3,-1,2) и прямую L: 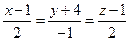(рис. Д. 1.2).

Уравнение искомой плоскости ищем в виде (1.3.1):

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0,

где (x₀, y₀, z₀) — координаты точки M₀(1, -4, 1), расположенной на прямой L и принадлежащей плоскости Р.

Вектор нормали 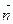к плоскости Р определим из условия

,

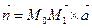где ,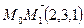

.

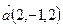
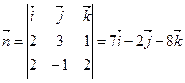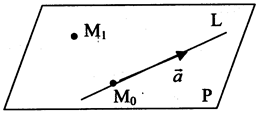
Рис. Д. 1.2

Таким образом, 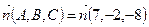и уравнение плоскости имеет вид

7(x – l) – 2(y + 4) – 8(z – l) = 0,

7x – 2y – 8z – 7 = 0.

Задача № 4. Найти расстояние между прямым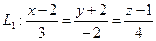и

и .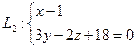

Прямая L₁ проходит через точку M₁(2, –2, l) и имеет направляющий вектор 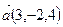. Уравнение прямой L₂ запишем в виде выражения (1.3.8),

предварительно определив какие-либо две точки, например: К₁(1,-6,0) и К₂(1,0,9), тогда

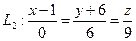или .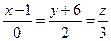

Направляющий вектор прямой L₂ 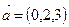. Прямые L₁ и L₂ не параллельны, т. к. 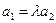, 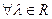. Проверим, пересекаются ли прямые L₁ и L₂, использовав условие (1.3.18)

.

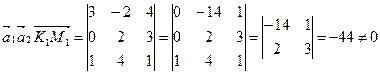Смешанное произведение векторов отлично от нуля, поэтому прямые L₁ и L₂ не пересекаются, а являются скрещивающимися прямыми. Расстояние между скрещивающимися прямыми находим по формуле (1.3.20), предварительно вычислив 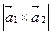по формулам (1.2.10) и (1.2.6):

;

.

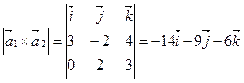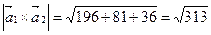Таким образом,

.

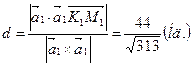Задача № 5. Вычислить значение многочлена f(А) от матрицы А, если

, .

.

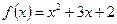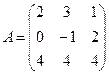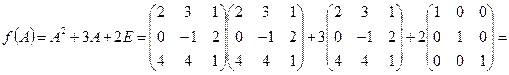
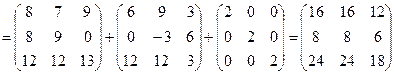Задача № 6. Матричным методом решить систему линейных алгебраических уравнений

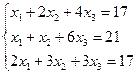
Решение системы находим по формуле (1.1.8): X = А^–1 В, где 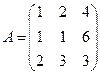, , 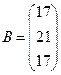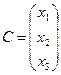а обратная матрица вычисляется по фор-

;

.

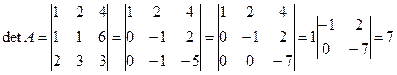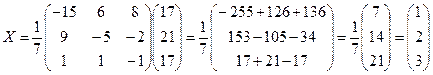Таким образом, x₁ = 1, х₂ = 2, х₃ = 3.

Задача № 7. Привести к каноническому виду уравнение линии второго порядка 3х² + 4ху – 4х – 8у = 0.

Определить тип кривой.

Решение задачи приведено в примерах 1.4.1 и 1.6.1. Метод решения студент выбирает сам.

Раздел 2. Дифференциальное исчисление функции одной переменной
Тема 2.1. Введение в анализ

Учебники: [16, гл. 1, §§ 1, 3,4], [4, гл. 1, 2, 3], [17, гл. 1, 2].

Аудиторная работа: [20, гл. 1, § 1 -4, М«1.20, 1.24, 1.36, 1.39, 1.186, 1.192, 1.203, 1.233, 1.241, 1.289, 1.299, 1.307, 1.324, 1.352], [15, гл. 5, §§ 2 - 8, №№ 673 (3), 682 (2), 700 (2), 703, 736, 739, 742, 750, 752, 756, 760, 767, 774, 784, 812 (2), 825 (1), 838, 842], [33, №№ 1.2, 1.5, 2.8, 2.11, 3.2, 3.11, 4.2, 4.3, 4.8, 5.4, 6.4, 7.5, 8.5, 9.5, 9.8, 10.8, 11.4, 11.6].

Самостоятельная работа: [20, гл. 1, §§ 1 - 4, №№ 1.19 - 1.27,1.28 - 1.42, 1.134 - 1.153, 1.182 - 1.190, 1.231 - 1.240, 1.272, 1.283, 1.288 - 1.312, 1.320 -1.332, 1.349 - 1.356, 1.365 - 1.370, 1.387 - 1.394], [15, гл. 5, §§ 1 - 8, №№ 673, 676 - 686, 734 - 800, 812, 825, 836 - 846], [33, №№ 1.1 - 11.13].

Дата добавления: 2014-11-20