Решение

Пример 2.1.5.

Решение.

; ; ; ; .

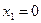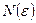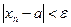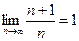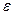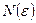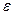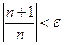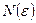Предел последовательности. Число а называется пределом последовательности , т. е. , если для любого существует номер такой, что при выполняется неравенство . При этом сама последовательность называется сходящейся, например, . Чтобы это доказать, достаточно указать способ построения для любого числа . Зададим и составим неравенство , которое эквивалентно неравенству . Если в качестве взять целую часть 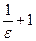, то для всех будет выполняться требуемое неравенство.

Вычисление пределов обычно проводится с использованием свойств сходящихся последовательностей.

.

.

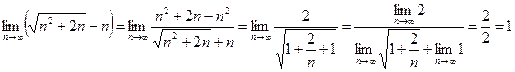Бесконечно малые величины. Переменная величина называется бесконечно малой величиной, если она в процессе своего изменения становится и остается по абсолютной величине меньше сколь угодно малого наперед заданного положительного числа. Примером может быть любая последовательность, сходящаяся к нулю.

Величина, обратная бесконечно малой, является бесконечно большой величиной.

Предел переменной величины. Переменная величина х в некотором процессе стремится к конечному пределу а, если х в этом процессе безгранично приближается к 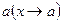, т. е. (х – а) есть величина бесконечно малая.

Для вычисления пределов важными являются их свойства.

Предел функции. Число А называется пределом функции f(x) в точке а и записывается 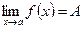, если для любого существует число 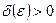такое, что из условия 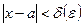следует неравенство .

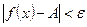В дальнейшем используются следующие замечательные пределы:

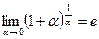, где е = 2.71828... - основание натуральных логарифмов.

Непрерывность функции. Функция у = f(x) непрерывна в точке х₀, если выполнены следующие условия:

а) функция определена в точке х₀ (существует f(x₀));

б) существует ;

в) .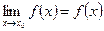

Если нарушено хотя бы одно из этих условий, то х₀ называют точкой разрыва.

Пример 2.1.6. 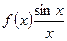не определена при х = 0, но — это точка устранимого разрыва.

Пример 2.1.7. — точка разрыва первого рода.

Пример 2.1.8. 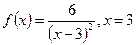— точка разрыва второго рода.

Для непрерывной функции знак функции и знак предела можно менять местами: .

Это свойство позволяет очень просто находить пределы непрерывных (в частности, элементарных) функций: отыскание предела функции сводится к вычислению значения функции в предельной точке.

Дата добавления: 2014-11-20