Указания. Тема 2.4. Комплексные числа

Тема 2.4. Комплексные числа

Вопросы для самопроверки

1. Перечислите различные типы неопределенностей, для раскрытия которых может быть использовано правило Лопиталя — Бернулли. Приведите примеры.

2. Напишите формулы Маклорена для функций е^х, sin x, cos x, (l + х)^а,
ln(1 + x).

3. Как найти наибольшее и наименьшее значения функции, дифференцируемой на замкнутом промежутке?

4. Как находятся интервалы выпуклости и вогнутости и точки перегиба? Приведите примеры.

Учебники: [16, гл. 8, §§ 1, 3], [4, гл. 5, §§ 5.3 - 5.5], [17, гл. 7].

Аудиторная работа. Решить примеры: [20, гл. 1, § 5, №№ 1.419, 1.422, 1.426, 1.468, 1.486, 1.499, 1.511, 1.515, 1.519, 1.527], [15, гл. 4, § 3, №№ 630 (4), 637, 634 (3), 645 (2), 655 (2)].

Самостоятельная работа: [20, гл. 1, § 5, №№ 1.418, 1.420, 1.421, 1.423 -1.429, 1.463 - 1.471, 1.496 - 1.498, 1.508 - 1.510, 1.512 - 1.515, 1.516 - 1.518, 1.520, 1.523 - 1.526], [15, гл. 4, § 3, №№ 630, 631 - 634, 636, 643, 644, 645, 657, 658].

Комплексные числа вводятся в рассмотрение либо как упорядоченная пара двух действительных чисел (х, у), либо как выражение вида x + iy, где , а i –символ, который называется мнимой единицей, удовлетворяющий равенству i2 = –1. При этом х называют вещественной частью, а y ‑мнимой, что записывается так: х = Re(x + iy), у = Im(x + iy).

Очень важна геометрическая интерпретация комплексных чисел. С ее помощью, в частности, получают различные формы записи: алгебраическую (x + iy), тригонометрическую 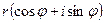и показательную 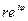, а также связь между ними.

Алгебраические действия над комплексными числами:

1. Сложение: (х₁ + iy₁) + (х₂ + iy₂) = x₁ + х₂ + i(y₁ + у₂);

2. Умножение: (х₁ + iy₁) + (х₂ +iy₂) = х₁х₂ – y₁y₂ + i(x₁y₂ + x₂y₁);

3. Деление: ;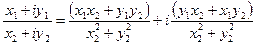

4. Возведение в целую степень: n раз;

5. Извлечение корня: число а + ib называется корнем n -й степени из числа x + iy, если и обозначается символом . Для всякого комплексного числа корень имеет n различных значений.

Например, 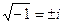, т.к. .

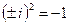Основная теорема алгебры комплексных чисел: всякий многочлен 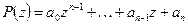с любыми коэффициентами 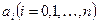степени 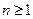имеет хотя бы один корень, в общем случае комплексный.

Из основной теоремы вытекает возможность разложения многочлена на линейные множители:

,

где z₁,z₂,...,z_k - все различные корни, — их кратности.

Для многочлена с вещественными коэффициентами имеет место разложение на вещественные линейные и квадратичные множители:

.

Например, .

Дата добавления: 2014-11-20