Указания. Данный раздел предполагает, что студент полностью овладел понятиями производной и дифференциала

Данный раздел предполагает, что студент полностью овладел понятиями производной и дифференциала. Он должен уметь:

а) находить производную и дифференциал от достаточно сложных элементарных функций;

б) находить производные и дифференциалы высших порядков от простейших элементарных функций.

Правило Лопиталя - Бернулли. Это правило является эффективным средством нахождения предела функции, когда возникают неопределенности. Так, если при функции 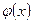и f(x) бесконечно малые или бесконечно большие, тогда их отношение не определено в точке х = а, и в этом случае говорят, что оно представляет собой неопределенность типа или . Однако, если существует предел отношения их производных, то к этому пределу будет стремиться и отношение самих функций.

Примеры:

.

К неопределенностям других видов правило Лопиталя — Бернулли применяется после преобразования их к виду или . Это можно сделать по схеме , и т. д.

К степенным неопределенностям можно применять это правило после их логарифмирования.

Формула Тейлора. Замена приращения функции дифференциалом дает возможность получить многие формулы приближенного вычисления функции. Эти формулы можно значительно уточнить, если применить дифференциалы высшего порядка: об этом и говорит формула Тейлора.

.

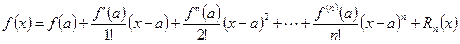Формула Тейлора позволяет вычислять значения функции с заранее заданной точностью. Например, используя формулу

посчитаем число е, ограничиваясь n = 7, получаем:

.

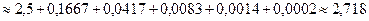Допускаемая при этом погрешность связана с отброшенным слагаемым R₇(1), так называемым остаточным членом формулы Тейлора.

В общей формуле Тейлора для остаточного члена имеется несколько форм записи:

— формаПеано;

— форма Л агранжа.

Так, в примере имеем 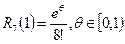, следовательно, погрешность .

Знание производной дает возможность изучать различные свойства функций. Наиболее простым вопросом является вопрос о возрастании и убывании функции, а также вопрос о локальных экстремумах. К ним примыкает и задача о нахождении наибольшего и наименьшего значений функции на замкнутом промежутке.

Построение графиков. Дифференциальное исчисление дает общий метод выявления индивидуальных особенностей заданной функции y = f(x), что позволяет строить график этой заданной функции быстрее и точнее, чем "по точкам". Так, нахождение интервалов монотонности функции и точек ее экстремума существенно при этом построении. Кроме того, полезными оказываются еще участки выпуклости и асимптоты. Обратим на них особое внимание, рассмотрев примеры.

Пример 2.3.1. Найти интервалы выпуклости и вогнутости, а также точки перегиба кривой Гаусса .

Решение. Находим первую и вторую производные:

, .

Приравняв нулю вторую производную, получим критические точки 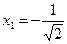, . Они разбивают числовую ось на три интервала: , , .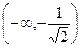

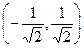Так как в первом и третьем интервалах у">0, то график вогнут при и при . Во втором интервале у"<0 (у"(0) = –2<0), то график выпуклый.

Точки с абсциссами являются точками перегиба (рис. 2.3.1)

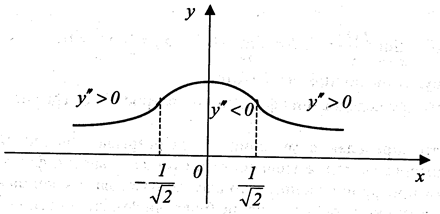
Рис. 2.3.1

Пример 2.3.2. Найти точку перегиба графика функции f(x) = х³.

Решение. f”(x) = 6x, f"(0) = 0, f”(–1) = –6 < 0, f"(l) = 6 > 0, следовательно, вторая производная меняет знак в точке (0,0), которая является точкой перегиба.

Пример 2.3.3. Найти точку перегиба графика функции . Решение. Находим производные:

,

Вторая производная в нуль нигде не обращается. Она не существует при х₀ = 1. Так как у" > 0 при х < 1 и у" < 0 при х > 1, точка (1,0) есть точка

перегиба. Касательная в этой точке параллельна оси ординат, т. к. первая производная при х = 1 обращается в бесконечность (рис 2.3.2)

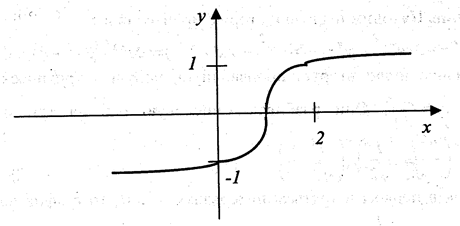
Рис. 2.3.2

Пример 2.3.4. Найти асимптоты кривой .

Решение. Так как , то прямая х = 0 является вертикальной асимптотой.

Если , , то прямая y = kx + b = x будет наклонной асимптотой.

Общая схема исследования функции и построения ее графика включает в себя поиск:

1) области определения функции, точек разрыва и нулей, после чего выясняются интервалы положительности и отрицательности функции, поведение функции при приближении к точкам ее разрыва и к концам интервалов, на которых функция определена, не будет ли функция четной, нечетной, периодической, находятся асимптоты графика и т.п.;

2) точек разрыва и нулей производной, после чего выясняются интервалы возрастания и убывания функции, точки экстремума и экстремальные значения;

3) точек разрыва и нулей второй производной, после чего выясняются участки выпуклости и вогнутости, а также точки перегиба, в которых полезно найти направление касательной.

Все найденные точки наносятся на координатную плоскость, после чего строится сам график, в поведении которого должны быть переданы все найденные индивидуальные особенности. Если из них поведение графика недостаточно ясно, то надо построить еще несколько точек графика, вычислив значения у’ для отдельных значений х; желательно также, вычислив значения у, найти в этих точках направление касательной.

Пример 2.3.5. Приведем в качестве примера исследование графика функции .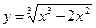

1) Область определения 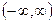. Функция имеет два нуля x₁ = 0, х₂ = 0, т. е. получается три интервала знакопостоянства; точек разрыва нет. Есть наклонная асимптота .

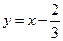2) Вычислив производную 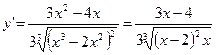, видим, что она имеет разрывы (обращается в ) при x₁ = 0 и х₂ = 2 и равна нулю при . Получается четыре интервала монотонности: 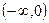, , , 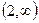и подстановка в y’ произвольных значений из этих интервалов показывает, что интервалом убывания будет только второй, а остальные — интервалы возрастания.

Таким образом, смена характера монотонности происходит при х = 0 (максимум с максимальным значением у = 0) и при (минимум с минимальным значением ).

3) Вычислив вторую производную, получим после преобразований . Она имеет разрывы там же, где и первая производная и не имеет нулей. Вторая производная меняет знак только в точке (2,0), которая является точкой перегиба. График вогнутый в интервале и выпуклый при х > 2. Вычислим также значения функции: при 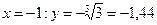; при х = 1, у = –1; при . Строим график (рис. 2.3.3).

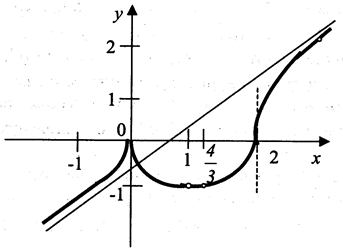
Рис, 2.3.3.

Дата добавления: 2014-11-20