Вопросы для самопроверки. 1. Показать, что есть расстояние между точками z1 и z2

1. Показать, что 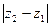есть расстояние между точками z₁ и z₂.

2. Доказать, что операция умножения обладает свойством коммутативности: z₁z₂=z₂z₁.

3. Доказать тождество и выяснить его геометрический смысл.

4. Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степеней из единицы.

5. Разложить многочлен х⁴ + 6х³ + 9х² +100 на простейшие множители, если один из его корней 1 + 2i.

Ответ: .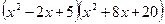

После изучения раздела 2 выполнить контрольную работу № 2.

Дополнение 2.1. Образец выполнения и оформления
контрольной работы № 2
"Дифференциальное исчисление функции одной переменной"

1. Найти пределы:

1)

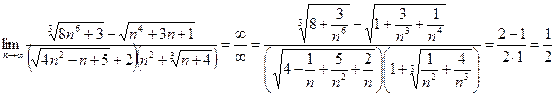
Ответ: ;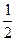

2) .

Ответ: ;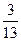

3)

.

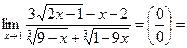
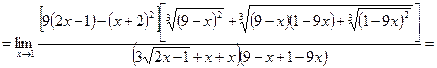
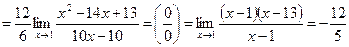Ответ: ;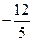

4) 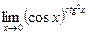, обозначим 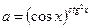, тогда

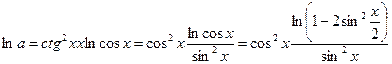
5) найдем предел этого выражения

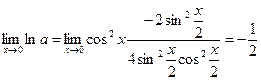, поэтому

Ответ: .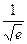

2. Найти производную данной функции 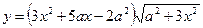и ее значение при х = а.

;

;

Ответ: ; .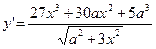

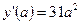3. Найти производную y = (2 + cos x)². Так как ln y = x ln(2 + cos x), то дифференцируя, получим:

,

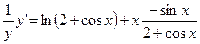или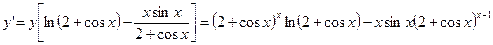

Ответ: .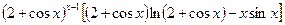

4. Найти уравнение касательной к кривой 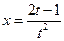, 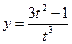в точке M(l,2). Уравнение касательной у – у₀ = к(х – х₀), где к = у’(х₀).

.

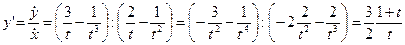Найдем значение t, соответствующее точке М: при х = 1, имеем 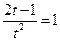, , , , 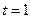т.е. 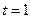. Значит 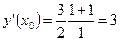, таким образом, у – 2 = 3(x – l).

Ответ: y = 3x – 1.

5. Найт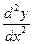и ,если , y = tg t – 1.

; .

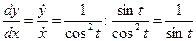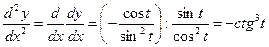Ответ: , .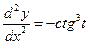

6. Найти пределы по правилу Лопиталя:

1)

.

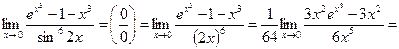
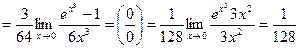Ответ: ;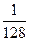

2) 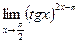, имеем неопределенность 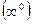. Пусть 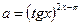, тогда 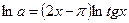, значит,

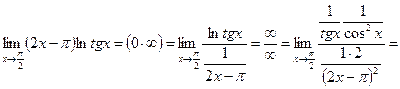
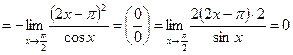, следовательно,

.

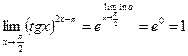Ответ: 1.

3) ,

.

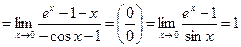Ответ: 1.

7. Разложить по формуле Тейлора f(x) = ln(2 + х – х²) в окрестности точки х₀ = 1.

Решение. .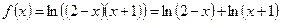

, ;

.

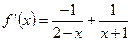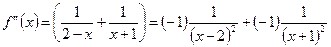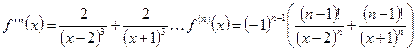Докажем по методу математической индукции:

.

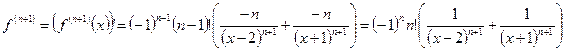Подставим в формулу

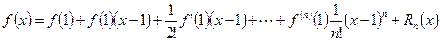значения производных, получим:

,

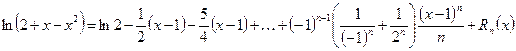где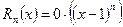

Остальные задания контрольной работы № 2 связаны с построением графиков функций. Эти вопросы полностью освещены в теме 2.3, в пункте "Построение графиков".

Раздел 3; Функции нескольких переменных

Дата добавления: 2014-11-20