Тема 3.1. Частные производные

Учебники: [16], [17].

Аудиторная работа: [3, №№3043 - 3083 нечет., 3124 - 3134 чет., 3145, 3147, 3149, 3181 - 3201 нечет.].

Самостоятельная работа: [3, №№3044 - 3084 чет., 3125 - 3135 нечет, 3146, 3148, 3150, 3152, 3182 - 3200 четные].

Назовем приращение функции по одной из переменных 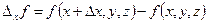частным приращением функции по переменной x.

Предел отношения частного приращения к приращению аргумента называется частной производной и обозначается

.

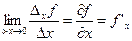Вычисляется частная производная по тем же правилам, что и производная от функции одной переменной, при этом остальные переменные считаются неизменными.

Если функция u = f(x,y,z), зависящая от трех переменных, которые, в свою очередь, зависят еще от переменных t и , т. е. и 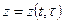, тогда

,

.

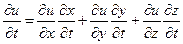Полный дифференциал первого порядка для функции многих переменных имеет вид

.

Производные высших порядков вводятся индуктивно, т. е. и т.п.

Производные 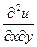, и т.д. называются смешанными произвонымн.

Полный дифференциал n –го порядка вычисляется по формуле

.

Если взять некоторое направление 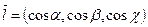, то производная от функции в этом направлении вычисляется следующим образом:

, где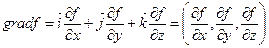

Пример 3.1.1. Вычислить производную функции 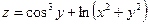в точке М₀(1,1) в направлении вектора .

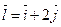Решение. По определению найдем в точке M₀(1,l). Для этого вычислим частные производные.

,

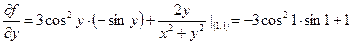
Из вектора 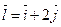сделаем единичный вектор

и окончательно получим:

.

Ответ: .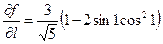

Пример 3.1.2. Найти второй дифференциал функции z, которая задана неявно: х³у + yz + z³ = 3.

Решение. По определению

.

От обеих частей функции, заданной в неявном виде, возьмем производную по х: , а затем еще раз производную по x: . Из этого равенства найдем :

.

Найдем смешанную производную ,. Равенство 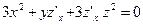дифференцируем по у:

;

.

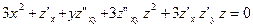От функции возьмем производную по у: . затем еще раз по у.

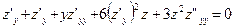
Из равенств 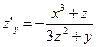; получим

,

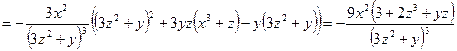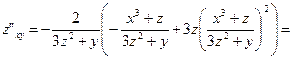
и окончательно запишем выражение для второго дифференциала

.

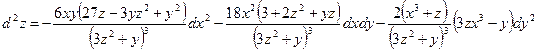Дата добавления: 2014-11-20