Решение. Следовательно, -1 < х < 5,т

, если .

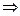
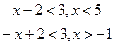Следовательно, -1 < х < 5,т. е. х меняется в интервале (-1,5).

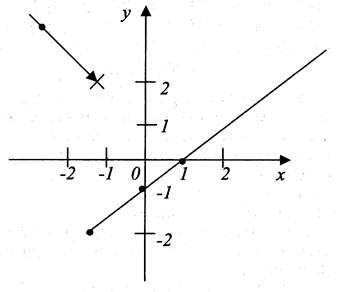
Пример 2.1.2. Построить график функции .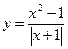

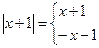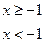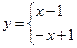Решение. Так как , если , то если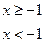

Строим график.

у = (–2) = 3

у(1) = 0, у(2) = 1, у(2) = –1

Множество — одно из наиважнейших понятий математики, которое вводится аксиоматически. Описательное пояснение: совокупность некоторых объектов, называемых элементами множества. Множества могут состоять из произвольных элементов, но каждое конкретное множество есть объединение (совокупность) элементов, имеющих общий для всех определенный признак (свойство). Например, множество целых чисел состоит из всех возможных целых чисел (быть целым числом - свойство для всех элементов множества).

Запись 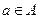означает, что объект a есть элемент множества А (принадлежит А), в противном случае пишут: . Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .

Запись 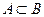(А содержится в В) означает, что каждый элемент множества А является элементом множества В. В этом случае множество А есть подмножеством множества В.

Множества А и В называют равными (А = В), есл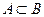и и .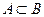

Существуют два основных способа задания множеств:

1. Множество А определяется непосредственным перечислением всех своих элементов a₁,a₂,…,a_n, т. е. записывается в виде ;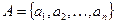

2. Множество А определяется как совокупность элементов из некоторого основного множества Т, которое обладает общим свойством а. В этом

случае используется обозначение , где запись 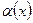означает, что элемент х обладает свойством .

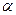Пример 2.1.3. Описать перечислением элементов множество

.

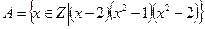Решение. А есть множество всех целых корней уравнения , следовательно, А = {-1,1,2}.

Объединением множеств А и В называется множество

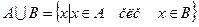
Пересечением множеств А и В называется множество

Разностью множеств А и В называется множество

Понятие функции. Пусть D — произвольное множество действительных чисел. Если каждому числу 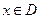поставлено в соответствие некоторое вполне определенное действительное число у, то говорят, что на множестве D определена числовая функция у = f(х). Множество D называется областью определения, а множество 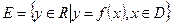— множеством значений числовой функции.

Наиболее распространенным является аналитический способ задания функции. Кроме него существуют еще табличный и графический.

Элементарные функции и их графики. Следующие функции называются основными элементарными:

1. Степенная функция: ;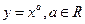

2. Показательная функция: ;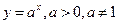

3. Логарифмическая функция: ;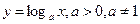

4. Тригонометрические функции:

y = sin x, y = cos x, y = tg x, y = ctg x;

5. Обратные тригонометрические функции:

у = arcsin х, у = arccos х, у = arctg х, у = arcctg x.

Элементарной называется функция, которая может быть получена из конечного числа основных элементарных функций с помощью арифметических операций и операции композиции.

Графиком функции у = f(x) называется множество

,

где R² — множество всех точек плоскости.

Понятие последовательности. Последовательностью действительных чисел называется числовая функция, определенная на множестве всех натуральных чисел у = f(n). Число f(n) называется n –м членом последовательности и обозначается символом x_n.

Пример 2.1.4. Написать первые пять членов последовательности

.

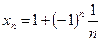Дата добавления: 2014-11-20