И построению ее графика

Приложение производной к исследованию функции

Вопросы для самопроверки

1. Что называется производной функции?

2. Каковы правила нахождения производных от суммы, произведения, дроби, от постоянной величины?

3. Как найти производную сложной функции?

4. Правило дифференцирования функции, заданной неявно.

5. В чем заключается метод логарифмического дифференцирования?

Методы дифференциального исчисления позволяют исследовать функции и строить их графики. Так, по знаку первой производной в интервале можно определить возрастание (убывание) функции, делать выводы о наличии или отсутствии экстремума функции. По знаку второй производной выделяем интервалы выпуклости (вогнутости) графика функции и точки перегиба ее графика.

Справедливы следующие теоремы:

1. Если функция дифференцируема на интервале и для 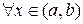, то эта функция возрастает (убывает) на интервале .

2. Если дифференцируемая функция 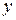= имеет экстремум в точке х 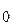, то ее производная в этой точке равна нулю: .

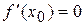3. Если непрерывная функция 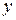= дифференцируема в некоторой 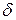-окрестности критической точки х 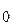и при переходе через нее (слева направо) производная 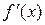меняет знак с плюса на минус, то х 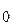- точка максимума; с минуса на плюс, то х 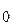- точка минимума.

4. Если функция 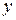= во всех точках интервала имеет отрицательную вторую производную, то график функции в этом интервале выпуклый верх; если 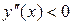, то график выпуклый вниз.

5. Если вторая производная 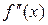при переходе через точку х 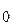, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х 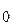- точка перегиба.

Построение графика функции значительно облегчается, если известны его асимптоты.

Различают 2 вида асимптот:

а) Вертикальные, существующие в точках разрыва второго рода. Их уравнения имеют вид .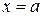

б) Наклонны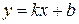е: , где

, .

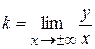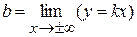В частности, при 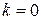наклонная асимптота становится горизонтальной и имеет уравнение .

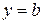При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:

1. Найти область определения функции.

2. Найти точки пересечения графика с осями координат, если это возможно.

3. Найти асимптоты графика функции.

4. Найти интервалы монотонности и точки экстремума функции.

5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

На основании полученного исследования построить график.

Пример 7 Исследовать функцию и построить ее график:

.

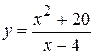Решение.

1. Область определения.

.

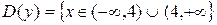2. Асимптоты графика:

а) вертикальная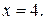

б) наклонная 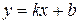, где

.

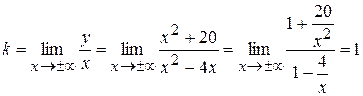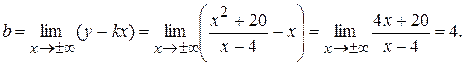
3. Найдем производную функции.

; ; .

.

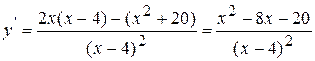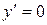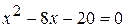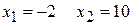Определим знак производной в промежутках:

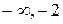	()	-2	-2, 4		(4, 10)		(10, + )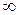
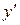
	+		-	не сущ.			+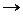
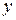
		max				min

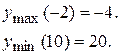
4. Найдем вторую производную функции.

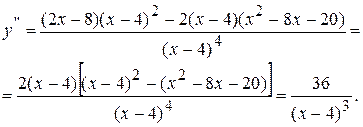
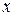
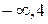	()		(4, + )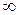
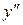
	-	не сущ.	+

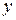
Точек перегиба графика функции нет.

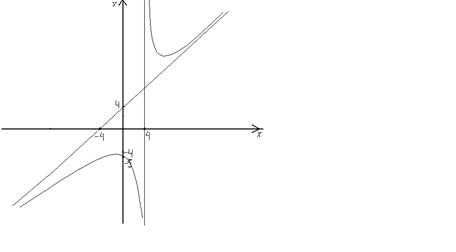По результатам исследования построим график функции.

Дата добавления: 2014-11-20