Интегрирование по частям. Метод замены переменного

Метод замены переменного

Пусть требуется найти неопределенный интеграл от непрерывной функции

Рассмотрим некоторую функцию 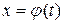, которая имеет непрерывную производную и обратную функцию . (Например: 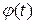монотонна). Тогда справедлива формула:

. (3.1.1)

В некоторых ситуациях удается подобрать функцию 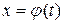так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:

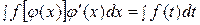. (3.1.2)

Другими словами, если подынтегральное выражение может быть записано в форме левой части (3.1.2), то с помощью подстановки получаем более простой интеграл (3.1.1).

Пример 8 .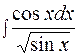

Решение.

.

Пример 9 .

На практике часто используется следующая простая формула:

,

где 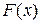- первообразная функции .

Пример 10. .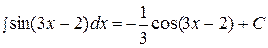

Пример 11. .

Пример 12. .

Формула интегрирования получается почленным интегрированием формулы производной произведения.

.

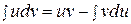Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный.

Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.

I.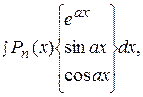

где 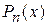- многочлен степени . В качестве нужно взять 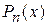, а 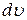= 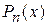- другой сомножитель.

При этом формулу приходится применить столько раз, какова степень многочлена.

II. .

В этом случае, наоборот, следует положить = .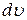

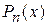Рассмотрим применение указанной схемы.

Пример 13.

.

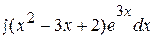Это интеграл первого типа, поэтому:

= =

= =

Пример 14. .

Решение.

Это интеграл второго типа, поэтому имеем:

.

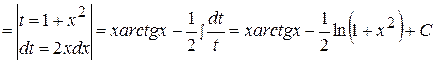Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию по ее дифференциалу . Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.

Формула интегрирования по частям может хорошо сработать и в других случаях.

Пример 15 .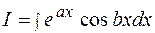

.

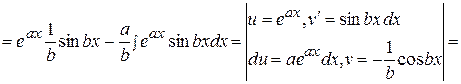
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим

,

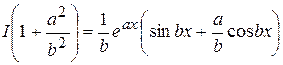откуда

.

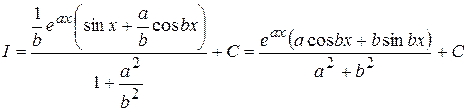Дата добавления: 2014-11-20