Логика и техника

Символическая логика широко применяется при описании и проектировании таких типов схем и механизмов, которые характеризуются прерывной, скачкообразной сменой конечного числа состояний – так называемым устройствам дискретного действия. К подобным устройствам относятся все цифровые вычислительные машины.

Использование логического аппарата возможно во всех устройствах, имеющих только два четко различимых состояния: «замкнуто – разомкнуто», «включено – не включено», «проводит ток – не проводит ток», «нажата кнопка – не нажата кнопка», то есть работающих по принципу «да – нет». Состоянию «да» соответствует состояние «контакт замкнут», что может быть описано символом «истина» или «1». Состоянию «нет» – «контакт разомкнут», символ «ложь» или «0». При этом 1 и 0 трактуются не как числа, с которыми можно производить арифметические действия, а как логические константы.

В современных устройствах используются параллельные или последовательные схемы. При последовательном соединении контактов каждый разряд фиксируется по очереди один за другим и проходит через одну линию. При параллельном соединении разряды фиксируются разными контактами и проходят через отдельные линии.

Последовательное соединение контактов Р и Q может быть выражено логическим И (конъюнкция). В релейно-контактной схеме при последовательном соединении контактов Р и Q ток в цепи пойдет, когда контакты в цепи замкнуты. Если же хотя бы один контакт разомкнут, то ток в цепи не пойдет. Также конъюнкция истинна лишь тогда, когда истинны все ее составляющие (см. рис. 17). В цифровых устройствах подобная функция (логическое И) часто используют для управления потоком информации.

Параллельное соединение контактов Р и Q можно может быть выражено логическим ИЛИ (слабая дизъюнкция). При параллельном соединении ток в цепи пойдет тогда, когда замкнут хотя бы один из контактов. Как известно, слабая дизъюнкция истинна тогда, когда истинно хотя бы одно входящее в ее состав простое высказывание (см. рис. 17).

Логическому НЕ (отрицанию) может быть поставлен в соответствие такой контакт в релейно-контактной схеме, который замкнут, когда нет токового сигнала, и который размыкается при подаче тока. Также отрицание высказывания р истинно, если исходное высказывание ложно и наоборот (см. рис. 16).

С помощью средств логики высказываний в технике решаются задачи:

– определение логической структуры устройства по заданным условиям его работы (логический синтез схемы дискретного действия);

– определение условий работы устройства по его известной логической структуре (логический анализ схемы дискретного действия).

Также часто возникает необходимость упрощения релейно-контактной схемы. Любая электрическая схема может быть записана в виде формулы, содержащей логические И, ИЛИ, НЕ (конъюнкцию, слабую дизъюнкцию, отрицание). Также любая формула логики высказываний может быть приведена к форме содержащей только эти логические союзы (нормальная форма формулы).

Для того чтобы минимизировать формулу, привести ее к нормальной форме используются равносильные формулы. Вот наиболее употребительные из них:

Закон двойного отрицания

А ≡ А

Законы коммутативности (симметричности) конъюнкции и дизъюнкции:

А ^ В ≡ В ^ А

А ˅ В ≡ В˅А

Законы ассоциативности конъюнкции и дизъюнкции:

А ^ (В ^ С) ≡ (А ^ В) ^ С

А ˅ (В ˅ С) ≡ (А˅ В) ˅ С

Законы дистрибутивности дизъюнкции относительно конъюнкции и конъюнкции относительно дизъюнкции:

А ˅ (В ^ С) ≡ (А ˅ В) ^ (А ˅ С)

А ^ (В ˅ С) ≡ (А ^ В) ˅ (А ^ С)

Законы идемпотентности конъюнкции и дизъюнкции:

А ^ А ≡ А

А ˅ А ≡ А

Законы де Моргана:

(А ^ В) ≡ А ˅ В

(А ˅ В) ≡ А ^ В

Законы поглощения:

А ^ (А ˅ В) ≡ А

А ˅ (А ^ В) ≡ А

Законы исключения

(А ˅ В) ^ (А ˅ В) ≡ А

(А ^ В) ˅ (А ^ В) ≡ А

Законы разложения

А ≡ (А ˅ В) ^ (А ˅ В)

А ≡ (А ^ В) ˅ (А ^ В)

Законы выявления:

(А ˅ С) ^ (В ˅ С) ≡ (А ˅ С) ^ (В ˅ С) ^ (А ˅ В)

(А ^ С) ˅ (В ^ С) ≡ (А ^ С) ˅ (В ^ С) ˅ (А ^ В)

Производные от законов выявления:

С ^ (В ˅ С) ≡ С ^ (В ˅ С) ^ В

(А ˅ С) ^ С) ≡ (А ˅ С) ^ С ^ А

Другие равносильности:

А ^ В ≡ (А ˅ В)

А ˅ В ≡ (А ^ В)

А → В ≡ (А ^ В)

А → В ≡ А ˅ В

А ↔ В ≡ (А ^ В) ^ (В ^ А)

А ↔ В ≡ (А ˅ В) ^ (В ˅ А)

А ^ В ≡ (А → В)

А ˅ В ≡ А → В

Сильная дизъюнкция заменяется слабой на основе равносильности:

А ˅ В ≡ (А ˅ В) ^ (А ˅ В)

А ↔ В ≡ (А → В) ^ (В → А)

А ↔ В ≡ (А ^ В) ˅ (В ^ А)

Закон контрапозиции:

А → В ≡ В → А

И ≡ Л

Л ≡ И

А ^ И ≡ А

А^ Л ≡ Л

А ˅ И ≡ И

А ˅ Л ≡ А

А ^ А ≡ Л

А ˅ А ≡ И

А → И ≡ И

И → А ≡ А

А → Л ≡ А

Л → А ≡ И

А ↔ И ≡ А

А ↔ Л ≡ А

Возможность подобного рода приложений логики обусловлена глубоким сходством отношений в логике высказываний и устройствах дискретного типа.

Упражнения

1. Преобразуйте формулы таким образом, чтобы они содержали:

а) (х → y) → (y ˅ z) – только конъюнкцию и отрицание;

б) (x ˅ y) ^ (x ˅ y) → (x ↔ y) ^ (x ↔ y) – только дизъюнкцию и отрицание.

2. По предложенным схемам составьте формулы и найдите условия работы (составьте таблицу истинности):

а)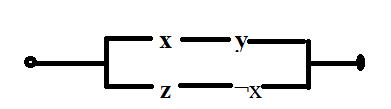

б)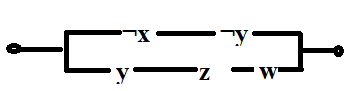

3. Постройте схемы по предложенным формулам:

а) p ^ (q ^ r ˅ p ˅ q);

б) p ^ q ˅ z;

в) (p ˅q) ^ r ˅p ^ r ˅ q.

4. Упростите схему:

а)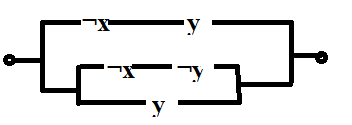

б)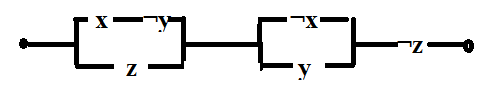

СЛОВАРЬ ТЕРМИНОВ

Аналогия – вероятностный вывод, в котором заключения о при­надлежности предмету определенного признака делаются на основе сходства существенных признаков с другими предметами.

Аргументация – приведение доводов (аргументов) в обоснование какого-либо тезиса.

Атрибутивное высказывание – высказывание, в котором ут­верждается или отрицается свойство или состояние предмета.

Высказывание – законченная мысль, которая является либо истинной, либо ложной.

Вывод – переход от посылок (исходных для одного или нескольких высказываний) к следствию (новому высказыванию, заключению) по правилам логики.

Дедукция – способ рассуждения, при котором осуществляется переход от знания общего к знанию частному или единичному.

Деление – логическая операция, посредством которой объем делимого имени (рода) подразделяется на ряд подмножеств (видов) с учетом избранного основания деления.

Диалектическая логика – учение о формировании и развитии знаний и применении их на практике.

Диалог – коммуникативный процесс, при котором люди взаимо­действуют посредством своих смысловых позиций.

Доказательство – вид аргументации, устанавливающий истинность тезисов на основе истинности аргументов дедуктивным путем.

Имя – слово или словосочетание, выражающее мысль о предмете с точки зрения его отличительных признаков.

Индукция – переход в процессе рассуждения от единичного или частного к общему.

Искусственный язык – язык, который строится по сформированным заранее правилам и предназначен для решения каких-либо конкретных задач.

Качество высказывания – указание на принадлежность или не­принадлежность признака, мыслимого в предикате, субъекту высказывания; определяется по характеру связки.

Количество высказывания – указание на то, что в атрибутивном высказывании что-то утверждается или отрицается об одном предмете, либо о части предметов, либо обо всех предметах определенного класса.

Логика – наука, которая исследует структуру мышления, раскрывает лежащие в его основе закономерности.

Логическая форма – способ связи содержательных частей рас­суждения.

Логическое значение сложного высказывания – истинность или ложность сложного высказывания, которое ставится в зависимость от логических значений (истинности либо ложности) простых высказываний.

Логический закон, или закон логики, – логическая форма, которая порождает истинное высказывание при любой подстановке переменных значений.

Логический квадрат – схема, позволяющая вывести определенные отношения по истинности и ложности простых высказываний, имеющих одинаковые термины и различающихся по качеству и количеству.

Мышление – активный процесс отражения объективного мира, имеющий опосредованный, обобщенный характер.

Непосредственный вывод – вывод, в котором заключение получается из одной посылки.

Объем имени – структурный компонент имени; совокупность предметов, обладающих специфическим для данного класса признаком.

Опосредованный вывод – вывод, в котором заключение получается из двух или более посылок.

Определение – логическая операция, раскрывающая содержание имени путем указания на его существенные признаки.

Опровержение – доказательство ложности тезисов, то есть истинности его отрицания.

Отношения между сложными высказываниями – отношения между логическими формами, которыми эти высказывания порождаются.

Парадокс – противоречие, возникающее в теории при соблюдении в ней логической правильности вывода.

Паралогизм – непреднамеренная логическая погрешность.

Полисиллогизм – вывод, представляющий собой цепь простых ка­тегорических силлогизмов, упорядоченных таким образом, что заключение одного силлогизма становится посылкой другого силлогизма.

Предикат высказывания – часть высказывания, в которой ото­бражается признак предмета мысли, его свойство, состояние, отношение.

Распределенность терминов – соотношение объемов субъекта и предиката высказывания; термин распределен, если его объем полностью входит в объем другого термина или полностью из него исключается.

Связка в высказывании – часть высказывания, указывающая на то, в каком взаимоотношении находятся термины высказывания.

Силлогизм простой категорический – дедуктивный опосредованный вывод, в котором две посылки – категорические высказывания, связанные общим термином.

Силлогистика – теория дедуктивных выводов.

Содержание имени – структурный компонент имени; совокупность признаков, на основании которых предметы обобщаются в классы.

Сорит – полисиллогизм, представляющий собой цепь энтимем.

Софизм – преднамеренная логическая ошибка, используемая с целью ввести кого-либо в заблуждение.

Субъект высказывания – часть высказывания, которая выража­ет предмет мысли.

Термины высказывания – субъект и предикат.

Формальная логика – наука о формах, в которых протекает че­ловеческое мышление, и о законах, которым оно подчиняется.

Формы мышления – понятие, суждение, умозаключение.

Энтимема – силлогизм с пропущенной посылкой или заключением.

Эпихейрема – сложносокращенный силлогизм, в котором посылками являются энтимемы.

Язык – знаковая система, используемая для коммуникации и познания.

Дата добавления: 2014-11-20