
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
L. Случайные величины
|
|
|
|
i. Случайная величина Х равна числу появлений «герба» в серии из n+3 бросаний монеты. Найти закон распределения и функцию распределения F(x) этой случайной величины; вычислить ее математическое ожидание M X и дисперсию D X; построить график F(x).
ii. Закон распределения дискретной случайной величины X имеет вид:
| xi | -2 | -1 | m | m+n | |
| pi | 0,2 | 0,1 | 0,2 | p4 | p5 |
Найти вероятности p4, p5, и дисперсию D X, если математическое ожидание M X =-0,5+0,5m+0,1n.
iii. Плотность распределения непрерывной случайной величины X имеет вид:

Найти:
а) параметр а; б) функцию распределения  ;
;
в) вероятность попадания случайной величины X в интервал
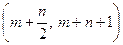 ;
;
г) математическое ожидание M X и дисперсию D X.
Построить график функций  и
и  .
.
iv. Случайные величины 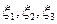 имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi=m+n, а дисперсия Dξ1=n2/3. Найти вероятности: а)
имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi=m+n, а дисперсия Dξ1=n2/3. Найти вероятности: а)  ; б)
; б) 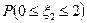 ; в)
; в)  .
.
13. Элементы математической статистики
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:
| № предприятия | Выпуск продукции | Прибыль | № предприятия | Выпуск продукции | Прибыль |
| 60+n | 15,7 | 52,0 | 14,6 | ||
| 78,0 | 18,0 | 62,0 | 14,8 | ||
| 41,0 | 12,1 | 69,0 | 16,1 | ||
| 54,0 | 13,8 | 85,0 | 16,7 | ||
| 60+n | 15,5 | 70+n | 15,8 | ||
| n•m+20 | n+m+10 | 71,0 | 16,4 | ||
| 45,0 | 12,8 | n•m+30 | n+m+20 | ||
| 57,0 | 14,2 | 72,0 | 16,5 | ||
| 67,0 | 15,9 | 88,0 | 18,5 | ||
| 80+n | 17,6 | 70+n | 16,4 | ||
| 92,0 | 18,2 | 74,0 | 16,0 | ||
| 48,0 | n+m+5 | 96,0 | 19,1 | ||
| 59,0 | 16,5 | 75,0 | 16,3 | ||
| 68,0 | 16,2 | 101,0 | 19,6 | ||
| 80+n | 16,7 | 70+n | 17,2 |
По исходным данным:
Задание 13.1.
13.1.1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
13.1.2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую  , среднее квадратическое отклонение
, среднее квадратическое отклонение 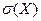 , дисперсию, коэффициент вариации V. Сделайте выводы.
, дисперсию, коэффициент вариации V. Сделайте выводы.
Задание 13.2.
13.2.1. Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.
13.2.2. Используя c2-критерий Пирсона, при уровне значимости 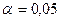 проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
Задание 13.3.
13.3.1. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.
13.3.2. Определите коэффициенты выборочного уравнения регрессии 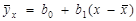 .
.
13.3.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
При расчетах целесообразно использовать стандартные математические пакеты для персональных компьютеров.
14. Линейное программирование
m. Задача оптимального производства продукции.
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, и С. Потребность 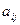 на каждую единицу
на каждую единицу  -го вида продукции
-го вида продукции  -го вида сырья, запас
-го вида сырья, запас  соответствующего вида сырья и прибыль
соответствующего вида сырья и прибыль  от реализации единицы
от реализации единицы  -го вида продукции заданы таблицей:
-го вида продукции заданы таблицей:
| Виды сырья | Виды продукции | Запасы сырья | |
| I | II | ||
| А | 
| 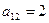
| 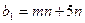
|
| В | 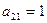
| 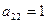
| 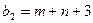
|
| С | 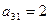
| 
| 
|
| прибыль | 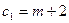
| 
| |
| план (ед.) | 
| 
|
i. Для производства двух видов продукции I и II с планом  и
и  единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее
единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее 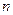 единиц обоих видов продукции.
единиц обоих видов продукции.
ii. В условиях задачи 14.1.1. составить оптимальный план  производства продукции, обеспечивающий максимальную прибыль
производства продукции, обеспечивающий максимальную прибыль 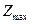 . Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
. Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
iii. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль 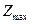 .
.
n. Транспортная задача.
На трех складах 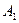 ,
,  и
и  хранится
хранится  ,
,  и
и 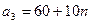 единиц одного и того же груза. Этот груз требуется доставить трем потребителям
единиц одного и того же груза. Этот груз требуется доставить трем потребителям 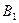 ,
, 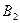 и
и 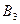 , заказы которых составляют
, заказы которых составляют  ,
, 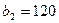 и
и 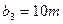 единиц груза соответственно. Стоимость перевозок
единиц груза соответственно. Стоимость перевозок 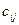 единицы груза с
единицы груза с  -го склада
-го склада  -му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
 потребности
запасы потребности
запасы
| 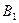
| 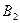
| 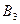
| |

| 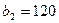
| 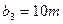
| ||
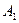
| 
|  4 4
|  2 2
|  
|

| 
|  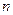
|  5 5
|  3 3
|

| 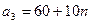
|  1 1
|  
|  6 6
|
i. Сравнивая суммарный запас 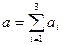 и суммарную потребность
и суммарную потребность 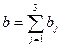 в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад 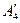 с запасом
с запасом 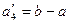 в случае
в случае  или фиктивного потребителя
или фиктивного потребителя 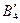 с потребностью
с потребностью 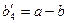 в случае
в случае  и положив соответствующие им тарифы перевозок нулевыми.
и положив соответствующие им тарифы перевозок нулевыми.
ii. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.)
iii. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
 ,
,
обеспечивающий минимальную стоимость перевозок 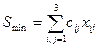 . Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 807; Нарушение авторских прав?; Мы поможем в написании вашей работы!