Економіко-математична ММБ

Основу інформаційного забезпечення ММБ становить технологічна матриця, що містить коефіцієнти прямих матеріальних витрат на виробництво одиниці продукції. Дана матриця є базою економіко-математичної ММБ. Припускається, що для виробництва одиниці продукції в 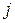-й галузі необхідна певна кількість витрат проміжної продукції -ї галузі, що становить 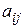. Ця величина не залежить від обсягів виробництва в 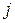-й галузі і є досить стабільною в часі. Величини 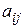називають коефіцієнтами прямих матеріальних витрат та обчислюють

.

(3)

Коефіцієнти прямих матеріальних витрат указують на те, яку кількість продукції -ї галузі необхідно витратити, якщо враховувати лише прямі витрати, для виробництва одиниці продукції 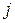-ї галузі.

З урахуванням (3) систему рівнянь (2) перепишемо у вигляді

.

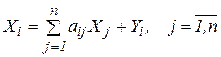(4)

Якщо ввести до розгляду матрицю коефіцієнтів прямих матеріальних витрат 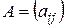, вектор-стовпчик валової продукції X та вектор-стовпчик кінцевої продукції Y: 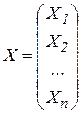, , 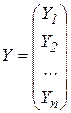то система рівнянь (4) у матричній формі матиме вигляд

.

(5)

Систему рівнянь (4) або у векторно-матричній формі (5) називають економіко-математичною моделлю міжгалузевого балансу (моделлю Леонтьєва, модель ¢¢витрати-випуск¢¢).

В основі даної моделі лежать наступні припущення:

1) в економічній системі виробляється, продається, закуповується, споживається та інвестується n продуктів;

2) кожна галузь є ¢¢чистою¢¢, тобто створює лише один продукт, сумісне виробництво різних продуктів виключається. Різні галузі випускають різні продукти;

3) під виробничим процесом кожної галузі розуміють перетворення деяких (можливо, всіх) типів продуктів у певний продукт. При цьому співвідношення використаного та випущеного продукту вважається сталим.

Величини X і Y у моделі (5) можуть бути представлені у натуральних або вартісних одиницях вимірювання, відповідно до цього розрізняють натуральний та вартісний міжгалузевий баланс.

Згідно з моделлю валовий випуск X розподіляється на дві частини: на виробниче споживання всіх галузей 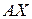і на кінцеве (невиробниче) споживання 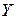. Кінцевий попит 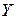складається з кінцевого споживання, експорту та інвестицій.

За допомогою моделі Леонтьєва виконують, як правило, три варіанти обчислень:

1) задаючи в моделі обсяги валової продукції кожної галузі 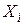, можна визначити обсяги кінцевої продукції галузі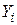

;

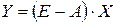(6)

2) задаючи обсяги кінцевої продукції всіх галузей 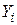, обчислюють обсяги валової продукції кожної галузі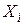

;

(7)

3) для низки галузей, задаючи обсяги валової продукції, а для решти — обсяги кінцевої продукції, можна відшукати величини кінцевої та валової продукції всіх галузей.

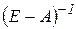У (6) — одинична матриця; — матриця, обернена до матриці . Якщо матриця не вироджена, тобто визначник 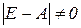, тоді існує обернена матриця 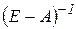, позначимо .

Умову (7) можна переписати у вигляді . Елементи матриці 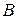позначають через 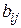. Тоді з матричного рівняння можна отримати . Згідно з даним співвідношенням валова продукція постає як зважена сума обсягів кінцевої продукції, валовими коефіцієнтами тут є 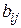, які вказують, скільки необхідно витратити валової продукції -ї галузі для випуску у сферу кінцевого використання одиниці продукції 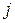-ї галузі. Коефіцієнти 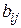називають коефіцієнтами повних матеріальних витрат, вони включають як прямі, так і опосередковані витрати всіх порядків. Якщо прямі витрати відбивають кількість засобів виробництва, застосованих безпосередньо для виготовлення певних обсягів даного продукту, то опосередковані стосуються попередніх стадій виробництва і входять у виробництво продукції не прямо, а через інші (проміжні) засоби виробництва.

Коефіцієнти повних матеріальних витрат 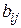указують, який обсяг продукції 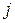-ї галузі необхідно виробити, щоб з урахуванням прямих та опосередкованих витрат цієї продукції одержати одиницю кінцевої продукції 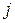-ї галузі.

Проаналізуємо величини, що входять у ММБ. Коефіцієнти матриці міжгалузевого балансу за визначенням є невід¢ємними, отже, матриця в цілому є невід¢ємною 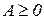. Процес відтворення не можна було б здійснити, якщо б для власного відтворення в галузі витрачався більший обсяг продукту, ніж створювався. Звідси очевидно, що діагональні елементи матриці менші, ніж одиниця: . З економічної точки зору вектори та 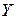складаються з невід¢ємних компонентів, тобто , . Постає питання: за яких умов економічна система здатна забезпечити невід¢ємний кінцевий випуск у всіх галузях? Відповідь на це питання пов¢язана з поняттям продуктивності ММБ, що еквівалентно продуктивності матриці коефіцієнтів прямих матеріальних витрат.

ММБ називається продуктивною, якщо вона є розв¢язною в невід¢ємних 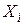, тобто .

Продуктивність матриці , відповідно і ММБ, пов¢язана з нерозкладністю матриці .

Матриця називається нерозкладною, якщо її не можна шляхом перестановок рядків і стовпців звести до вигляду 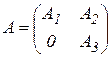, де — квадратні матриці. Нерозкладність технологічної матриці означає, що кожна галузь хоча б опосередковано використовує продукцію всіх галузей.

Для нерозкладної матриці має місце теорема Фробеніуса-Перрона:

1) нерозкладна матриця має додатне власне число 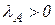, що перевищує модулі всіх інших власних чисел;

2) власному числу відповідає єдиний власний вектор 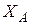(із точністю до скалярного множника), всі координати якого ненульові та мають один знак (тобто його завжди можна вибрати додатним за рахунок скалярного множника).

За допомогою теореми Фробеніуса-Перрона є змога довести таку теорему:

Модель Леонтьєва продуктивна тоді й тільки тоді, коли .

Достатність

Оскільки 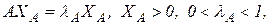то

, тому

. Але 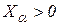, , звідси .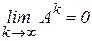

Розглянемо наступну математичну рівність:

.

Оскільки границя правої частини при дорівнює , то наявна й границя лівої частини. Таким чином, 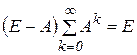, тобто обернена матриця 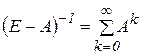існує, і для неї має місце розклад, аналогічний сумі неокласичної геометричної прогресії. Крім того, оскільки , то , тому для будь-якого вектора кінцевого попиту дійсний невід¢ємний розв¢язок системи рівнянь

.

Тобто модель Леонтьєва продуктивна.

Необхідність

Нехай модель Леонтьєва продуктивна. Тоді для вектора кінцевого попиту 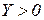існує такий вектор валового випуску , що , тобто і відповідно 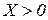. Помножимо останню нерівність на вектор-рядок 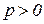, тоді

, але 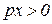, тому . Œ

Аналізуючи подане доведення теореми, знаходимо, що, крім безпосереднього обчислення матриці повних витрат , її ще можна розкласти у ряд

.

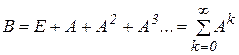Остання теорема дає змогу перевірити модель Леонтьєва на продуктивність, однак її формулювання не піддається прямій економічній інтерпретації.

Більш практичною є наступна достатня умова продуктивності. Якщо технологічна матриця нерозкладна, сума елементів кожного рядка не перевищує одиниці: , і якщо б для одного рядка , то модель Леонтьєва продуктивна.

Доведення. Нехай — власний вектор матриці , що відповідає власному числу , тобто , помножимо останню рівність справа на вектор-стовпчик , отримаємо .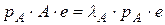

Оскільки 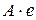— , то ліва частина останньої рівності за умовою теореми , але права частина дорівнює 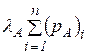, тому , тобто модель Леонтьєва продуктивна. Œ

Якщо модель Леонтьєва продуктивна, то для будь-якого вектора кінцевого попиту однозначно обчислюється невід¢ємний вектор валового випуску за формулою . Цей розклад означає, що для даного обсягу кінцевого продукту 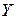необхідно використати продуктів, але спочатку їх слід виготовити, для чого потрібно продуктів, для виробництва яких у свою чергу необхідно 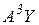продуктів і т.д.

Розглянуті умови продуктивності матриці можна сформулювати інакше (дане формулювання буде еквівалентним вищерозглянутому): для того щоб матриця коефіцієнтів прямих матеріальних витрат була продуктивною, потрібно і достатньо, щоб виконувалась одна з умов:

1) матриця невід¢ємно обернена, тобто існує обернена матриця ;

2) матричний ряд 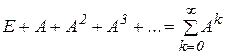збігається, а його сума дорівнює оберненій матриці ;

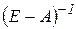3) найбільше за модулем власне число матриці , тобто розв¢язок характеристичного рівняння строго менший від одиниці;

4) усі головні мінори матриці додатні;

5) норма матриці , тобто величина найбільшої із сум елементів матриці в кожному стовпчику, строго менша за одиницю — достатня умова продуктивності матриці .

Розглянемо коефіцієнти повних матеріальних витрат. Найбільший за модулем корінь характеристичного рівняння в умові 3 продуктивності матриці (позначимо ) може служити оцінкою загального рівня коефіцієнтів прямих матеріальних витрат, відповідно величина характеризує залишок після витрат, тобто продуктивність. Чим більше , тим більше можливостей для досягнення інших цілей, крім поточного виробничого споживання. Іншими словами, чим вищий загальний рівень коефіцієнтів матриці , тим більше за модулем власне число і нижчий рівень продуктивності, й навпаки, чим нижчий загальний рівень коефіцієнтів матриці , тим менше за модулем найбільше власне значення та вища продуктивність.

Згідно з визначенням матриці повних матеріальних витрат її коефіцієнти показують, скільки всього необхідно виготовити продукції -ї галузі для того, щоб отримати одиницю кінцевої продукції 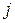-ї галузі.

Дають інше визначення коефіцієнта повних матеріальних витрат, виходячи з того, що, крім прямих витрат, існують опосередковані витрати тієї чи іншої продукції при виробництві сукупності товарів даної галузі. У якості прикладу розглядають технологічний ланцюг ¢¢руда-чавун-сталь-прокат¢¢. Витрати електроенергії при отриманні прокату із сталі будуть називатися прямими витратами, ті ж витрати при одержанні сталі із чавуну будуть називатися опосередкованими витратами 1-го порядку, витрати електроенергії для отримання чавуну з руди називатимуть опосередкованими витратами електроенергії на випуск сталевого прокату 2-го порядку і т.д. У зв¢язку із цим дамо наступне визначення.

Коефіцієнтом повних матеріальних витрат називається сума прямих та опосередкованих витрат продукції -ї галузі для виробництва одиниці продукції 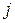-ї галузі через усі проміжні продукти на всіх попередніх стадіях виробництва. Якщо коефіцієнт опосередкованих матеріальних витрат 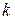-го порядку позначити через , то має місце формула

.

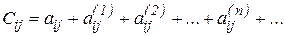(8)

Якщо ввести в розгляд матрицю коефіцієнтів повних матеріальних витрат і матриці коефіцієнтів опосередкованих матеріальних витрат різних порядків 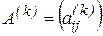, то умову (8) можна переписати у матричному вигляді

.

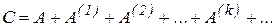(9)

Виходячи зі змісту коефіцієнтів опосередкованих матеріальних витрат, можна записати ряд матричних співвідношень:

.

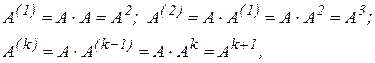з використанням яких умова (9) набуває вигляду

.

(10)

Якщо матриця коефіцієнтів прямих матеріальних витрат є продуктивною, то з умови продуктивності постає матриця , котра є сумою збіжного матричного ряду

.

(11)

Порівнявши формули (10) та (11), можна встановити зв¢язок між двома матрицями коефіцієнтів повних матеріальних витрат

, або в поелементній формі запису

Дана умова визначає економічний сенс різниці між коефіцієнтами матриць 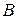і : на відміну від коефіцієнтів матриці , що враховують лише витрати на виробництво продукції, коефіцієнти матриці 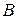містять, окрім витрат, також саму одиницю кінцевої продукції, котра виходить за сферу виробництва.

Дата добавления: 2014-12-08