Динамічна рівновага системи

Основним предметом дослідження в даній моделі економіки є можливість існування ситуації динамічної рівноваги в системі. У зв¢язку із цим серед траєкторій розвитку системи (1), (2) можна виділити клас стаціонарних траєкторій, тобто таких, на яких відбувається зростання з постійним темпом, відповідно ця траєкторія може бути подана у вигляді

У рамках даних співвідношень і на основі умов (1), (2) розглядаються дві взаємодвоїсті задачі оптимізації темпів зростання:

(3)

де — темп зростання економіки;

(4)

У задачі (3) необхідно знайти максимально можливий технологічний темп зростання системи, сталий у часі , і відповідний йому вектор інтенсивності. Технологічний темп системи, що описується моделлю Неймана, визначається так:

.

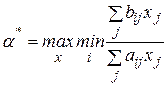траєкторії, на яких усі компоненти вектора зростають із темпом, більшим або рівним заданому, називаються рівноважними траєкторіями. Таким чином, стаціонарні траєкторії є рівноважними, а задача (3) полягає у відшуканні максимально можливого темпу зростання для рівноважної траєкторії.

У задачі (4) розглядаються коефіцієнти рентабельності способів виробництва такого вигляду:

,

котрі характеризують ефективність 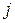-го базисного процесу при заданих цінах 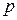. Коефіцієнт також указує, в скільки разів можуть бути збільшені витрати, щоб виробничий процес залишався незбитковим. Розв¢язок задачі (4) визначається співвідношенням

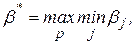
де 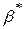— економічний темп зростання системи.

Слід відзначити, що характеризує процентну ставку на капітал чи накопичення (нагромадження) основних виробничих фондів (ОВФ) в економіці, яке визначається цією процентною ставкою, а темп накопичення капіталу характеризується величиною такої ставки.

Окремим питанням у контексті моделі Неймана є таке: чи можлива рівновага в системі та який у ній буде темп зростання при постійних цінах і постійній (сталій) ставці на капітал. Ці моделі отримали назву моделей із нульовим прибутком, а умова 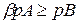називається умовою нульового прибутку.

Нейманом було доведено існування розв¢язків задач (3), (4) при достатньо вагомих умовах: 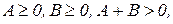причому встановлено існування єдиного темпу зростання , для котрого .

Якщо на матриці накладені незначні обмеження, то може існувати декілька рівноважних траєкторій із різними темпами зростання, серед яких одна є магістраллю — рівноважна траєкторія з максимальним темпом зростання. Промінь, що проходить через рівноважний вектор інтенсивностей, називають променем Неймана.

Залежно від знайденого темпу зростання поведінку економічної системи, яка описується моделлю Неймана, можна поділити на такі класи:

— відповідає розширеному відтворенню;

— простому відтворенню;

— звуженому відтворенню.

Якщо в системі має місце розширене відтворення, то це означає, що модель продуктивна: існує такий вектор 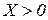, що .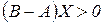

Важливість результату аналізу теоретичних моделей розширюваної економіки, до котрих належить і модель Неймана, полягає в доведенні існування магістралі-траєкторії максимального пропорційного зростання, тобто з постійним у часі максимально можливим зростанням та незмінною структурою виробництва.

Магістраль не залежить від тривалості планового періоду і є ефективною траєкторією для будь-якого скінченного інтервалу часу.

Стосовно широкого класу моделей економічної динаміки, доводяться теореми про магістраль. Теореми про магістраль — це твердження про те, що за умови достатньої тривалості планового періоду оптимальна траєкторія динамічної моделі незалежно від початкового стану та цільової функції або за даного кінцевого стану в тому чи іншому значенні близька до магістралі. Модель, для якої справедлива теорема про магістраль, називається магістральною моделлю.

Існують різні класифікації теорем про магістраль. Найбільш розповсюдженим є їх поділ на теореми про магістраль у слабкій, сильній і найсильнішій формі. Перші встановлюють лише факт близькості (за кутовою відстанню) більшості точок траєкторії до точок магістралі. У теоремах про магістраль у сильній формі йдеться про те, що точки, далекі від магістралі, можуть належати тільки до початку та кінця кожної оптимальної траєкторії. Теореми про магістраль у найсильнішій формі встановлюють, що більшість точок траєкторії лежать на магістралі.

Доведено існування магістралі для моделі Неймана. Промінь Неймана, започаткований вектором , котрий задовольняє умову,

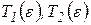є магістраллю моделі Неймана, якщо для будь-якого існують такі числа , що для якої завгодно оптимальної траєкторії

тобто майже весь час будь-яка оптимальна траєкторія йде вздовж променя Неймана, котрому відповідає вектор .

Дата добавления: 2014-12-08