Модель Неймана— модель економічного зростання

Модель Неймана

Лекція №10

Контрольні запитання

1. У чому полягає суть моделі міжгалузевого балансу?

2. Схарактеризувати складові частини схеми міжгалузевого балансу

виробництва.

3. Які припущення лежать в основі моделі Леонтьєва?

4. Які обчислення виконюють за допомогою моделі Леонтьєва?

5. Яка модель називається продуктивною? Яка матриця вважається нерозкладною? Сформулювати теорему Фробеніуса-Перрона.

6. Які Ви знаєте приклади застосування міжгалузевого балансу для аналізу трудових ресурсів, фондів?

7. Які витрати розуміють під поняттям повних затрат праці?

8. У чому полягає економічний сенс основного балансового рівняння в теорії міжгалузевого балансу праці?

1. Модель Неймана — модель економічного зростання.

2. Динамічна рівновага системи.

Найвідомішою моделлю економічного зростання є модель Неймана. В основі її лежить поняття технології. Нехай 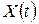— 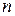- вимірний вектор витрат у момент часу 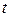; 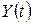— вектор випуску в момент часу 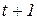. Пара 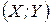утворює технологічний процес (технологію), якщо, використовуючи технологію періоду 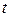, можна отримати із залучених у виробництво в момент часу 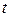ресурсів вектор випуску 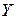у момент часу 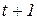. Усі технологічні процеси 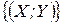утворюють виробничо-технологічну множину. Якщо 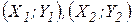— пара технологій, то кажуть, що 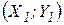більш ефективна, ніж 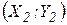, коли 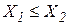і . 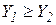Технологія 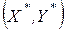є результативною (оптимальною за Парето), якщо не існує більш ефективної технології.

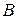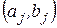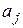Час у моделі є дискретним. Вона визначається парою матриць і . За допомогою цих матриць описується виробничо-технологічна множина моделі Неймана. Вона задається за допомогою скінченного набору виробничих процесів. Кожен виробничий процес визначається парою векторів , де — вектор витрат продуктів; 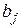— вектор випуску продукції 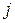-м технологічним процесом за умови одиничної інтенсивності його функціонування.

Нехай 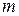процесів виготовляють 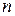продуктів та задані деякі технологічні процеси, назвемо їх базисними. Уведемо — матриця витрат, у якій стовпці є векторами 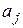базисних процесів, що складаються з елементів 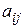— витрат -го продукту в 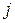-му виробничому способі при одиничній інтенсивності функціонування. Відповідно стовпці матриці випуску 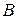— вектори 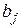базисних виробничих процесів, отже, 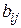— випуск -го продукту 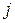-им виробничим процесом при одиничній інтенсивності його функціонування. Матриці і 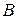сталі в часі та відображають рівень виробничої технології в системі.

На матриці витрат і випуску накладаються такі обмеження:

1. , , .

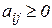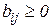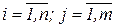2. Кожен виробничий спосіб використовує хоча б один вид витрат .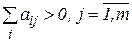

3. Кожен продукт випускається хоча б одним способом .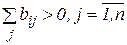

Якщо в рядку матриці 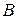більше від одного елемента, відмінного від нуля, то продукт може бути виготовлений більш ніж одним способом, і навпаки — виробничий спосіб може характеризуватися випуском кількох продуктів. У цьому полягає суттєва відмінність моделі Неймана від моделі Леонтьєва.

Змістовність моделі та її розв¢язність забезпечуються наступними припущеннями:

1. У моделі Неймана розглядається лише виробниче споживання. Коефіцієнти матриці 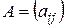відмінні від коефіцієнтів моделі Леонтьєва тим, що в них ураховано не лише споживання -го продукту 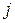-м виробничим способом, але й споживання -го продукту, необхідне для здійснення даного виробничого процесу. Таким чином, у модель Неймана включаються витрати на відтворення праці.

2. Усі доходи інвестуються.

3. Оплата праці підтримується на рівні прожиткового мінімуму, який визначається з виробничої необхідності.

4. У моделі Неймана всі ресурси вважаються відтворюваними.

Для опису моделі вводяться такі позначення:

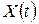— вектор інтенсивностей базисних процесів на інтервалі часу ;

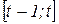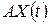— вектор витрат у 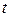-й період;

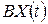— вектор випуску в 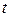-й період;

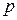— вектор цін на продукцію;

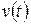— ціна + норма ренти за -й продукт у період .

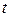Нехай відомі величини 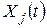і 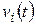. Тоді величина запасу -го продукту в кінці періоду 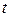, готового до виробничого споживання в період 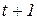, складає

.

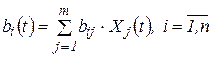Звідси випливає, що інтенсивності 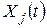у період 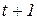повинні задовольняти обмеження

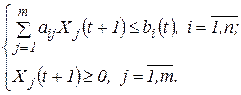
Або у векторно-матричній формі

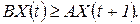
(1)

Повна вартість випуску 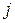-го процесу за умови одиничної інтенсивності його функціонування дорівнює

.

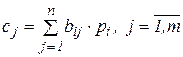Оцінки 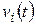усіх спожитих продуктів у грошовому вираженні в 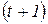-му періоді повинні задовольняти обмеження

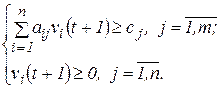
Або у векторно-матричній формі

,

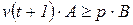(2)

де 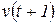, 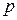— вектор-рядки.

Дата добавления: 2014-12-08