Ход уроков

III. Самостоятельная работа.

Вариант I.

1. Раскройте скобки и найдите значение выражения:

а) – 0,56 + (3,8 – 2,44); б) – 3,24 – (– 4,76 – 2,9);

в) .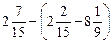

2. Упростите выражение (с + 5,4) – (4,9 + с).

3. Решите уравнение – 5,4 – (х – 7,2) = 1,9.

Вариант II.

1. Раскройте скобки и найдите значение выражения:

а) – 0,37 + (4,2 – 4,63); б) – 13,96 – (– 15,87 – 2,51);

в) .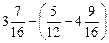

2. Упростите выражение (п – 5,8) – (4,9 + п).

3. Решите уравнение – 8,9 – (3,7 – х) = –13,6.

Домашнее задание: повторить все правила, решить № 1255 (г; е), № 1256 (в – д), № 1257 (а; б), № 1259 (б).

I. Повторение ранее изученного материала.

1. Сформулировать определения медианы, биссектрисы и высоты треугольника.

2. Равнобедренный треугольник и его свойства. Признаки равенства треугольников.

3. Определение средней линии треугольника и ее свойство.

4. Теорема Пифагора и обратная ей теорема.

5. Формула для вычисления площади треугольника.

6. Понятие параллелограмма, свойства и признаки параллелограмма, ромба, прямоугольника.

7. Определение трапеции, виды трапеций.

8. Площадь параллелограмма, площадь трапеции.

II. Решение задач.

Повторение можно организовать в ходе решения следующих задач:

1. В треугольниках ABC и A ₁ B ₁ C ₁ дано AB = A ₁ B ₁; AC = A ₁ C ₁, точки D и D ₁ лежат соответственно на сторонах BC и B ₁ C ₁; AD = = A ₁ D ₁. Докажите, что данные треугольники равны, если AD и A ₁ D ₁: а) высоты; б) медианы.

Примечание. при решении задачи 1 (б) полезно обратить внимание учащихся на прием «удвоения медианы» – откладывание на продолжении медианы AD за точку D отрезка, равного медиане.

2. Докажите, что центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию.

3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к его основанию, или на ее продолжении.

4. Докажите, что треугольник является равнобедренным, если две его медианы равны.

5. Докажите, что если в треугольнике две высоты равны, то центр вписанной в него окружности лежит на одной из медиан этого треугольника, а центр описанной окружности – на той же медиане или ее продолжении.

6. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.

7. Докажите, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.

8. Найдите длины отрезков, соединяющих середины сторон трапеции с равными диагоналями, если ее основания раны 7 см и 9 см, а высота равна 8 см.

9. Вычислите площадь треугольника АВС, если AB = 8,5 м, АС = 5 м, высота АN = 4 м и точка N лежит на отрезке BC.

10. Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны по 6 дм и пересекаются под углом 60°. Вычислите площадь четырехугольника ABCD.

Дата добавления: 2014-12-08