
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинематика
|
|
|
|
МЕХАНИКА
Задача № 1 ( 2 балла ) Решение: (РОФ, 2008)
 |
Так как
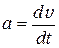 , то
, то 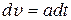 . Таким образом, везде, где а > 0 (т.е. для всех точек графика!) скорость увеличивается, при этом её величина равна площади под графиком зависимости скорости от времени υ (t).
. Таким образом, везде, где а > 0 (т.е. для всех точек графика!) скорость увеличивается, при этом её величина равна площади под графиком зависимости скорости от времени υ (t).
Задача № 2 ( 6 баллов ) Решение: (РОФ, 2007)
Так как Меркурий планета, ближайшая к Солнцу, то ее наблюдению с Земли мешает солнечный свет. Меркурий может быть виден либо утром, перед восходом Солнца, либо вечером, сразу после заката. Оптимальные условия наблюдения Меркурия реализуются, когда он находится на максимальном угловом удалении от Солнца, т.е. когда угол между направлениями на планету и на Солнце с Землей максимален. Пусть 11сентября 2008 г. Земля находится в точке 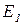 , тогда Меркурий находится в точке
, тогда Меркурий находится в точке 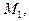 такой, что прямая
такой, что прямая 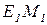 является касательной к орбите Меркурия. К 4 января 2009г. (т.е. через время
является касательной к орбите Меркурия. К 4 января 2009г. (т.е. через время 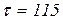 суток) Земля сместится в точку
суток) Земля сместится в точку 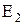 , повернувшись вокруг Солнца на угол
, повернувшись вокруг Солнца на угол 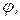 причем
причем 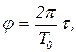 (1), где
(1), где 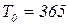 суток – период обращения Земли вокруг Солнца. За этот же промежуток времени Меркурий сместится в точку
суток – период обращения Земли вокруг Солнца. За этот же промежуток времени Меркурий сместится в точку 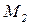 , сделав еще один полный оборот вокруг Солнца, т.е. угол поворота Меркурия вокруг Солнца равен
, сделав еще один полный оборот вокруг Солнца, т.е. угол поворота Меркурия вокруг Солнца равен 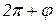 , следовательно,
, следовательно, 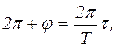 (2), где
(2), где 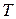 – искомый период обращения Меркурия.
– искомый период обращения Меркурия.
Из уравнений (1) – (2) можно найти 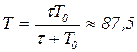 суток. Отметим, что из (1) – (2) получается известное в астрономии соотношение между сидерическим (истинным)
суток. Отметим, что из (1) – (2) получается известное в астрономии соотношение между сидерическим (истинным) 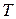 и синодическим (наблюдаемым)
и синодическим (наблюдаемым) 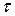 периодом обращения
периодом обращения
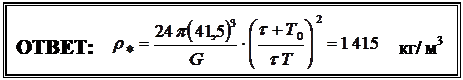 |
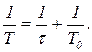 Так как
Так как 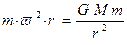 , где
, где 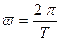 , то получим:
, то получим:
Задача № 3 ( 5 баллов ) Решение: (ОФ, 2009)
Обозначим угловую скорость вращения секундной, минутной и часовой стрелок часов соответственно - ωс, ωм, ωч.Угол поворота каждой стрелки часов равен 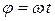 , то есть:
, то есть: 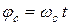 (1),
(1), 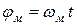 (2),
(2), 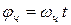 (3). Периоды вращения соответствующих стрелок равны:
(3). Периоды вращения соответствующих стрелок равны:
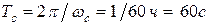 ,
, 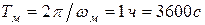 ,
, 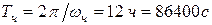
Начиная с полночи, когда положение всех стрелок совпадает, через определённый отрезок времени tx все они повернутся на один и тот же угол и на разное число целых оборотов. При этом будут выполняться следующие равенства:
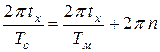 ,
, 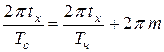 ,
, 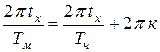 или
или
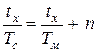 (4),
(4), 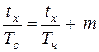 (5),
(5), 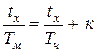 (6) или
(6) или
Из (4) – (6) получим:
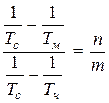 ,
, 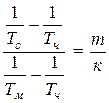 или
или 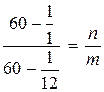 ,
, 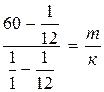 .
.
Таким образом, получим два уравнения в целых числах:
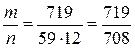 (7),
(7), 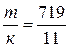 (8).
(8).
Из (8) получим к = 11 ℓ и m = 719 ℓ, где ℓ- целое число и ℓ
Из (6) выразим искомое время через которое совпадут стрелки часов:
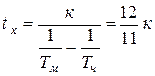 (9)
(9)
Искомое время tx не должно быть больше суток (иначе решения, очевидно, нет). Следовательно, 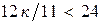 или.
или. 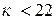 . Поскольку к = 11 ℓ, то ℓ = 0 и 1, что соответствует значениям tx = 0 и 12 часов. Другими словами после полуночи следующий раз совпадение стрелок произойдёт в полдень и так далее три раза за полные сутки. В течении недели за 7 суток кукушка покажется из часов 1 + 2 , 7 = 15 раз.
. Поскольку к = 11 ℓ, то ℓ = 0 и 1, что соответствует значениям tx = 0 и 12 часов. Другими словами после полуночи следующий раз совпадение стрелок произойдёт в полдень и так далее три раза за полные сутки. В течении недели за 7 суток кукушка покажется из часов 1 + 2 , 7 = 15 раз.
В том случае, если часы звучат через отрезок времени ty при встрече двух стрелок- минутной и секундной, то из (4) получим 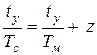 , где z – целое число или
, где z – целое число или 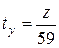 (10). За время одного оборота минутной стрелки, то есть за 1 час таких отрезков времени, должно быть целое число N (время между любыми последовательными моментами совпадения стрелок постоянно). Таким образом, запишем:
(10). За время одного оборота минутной стрелки, то есть за 1 час таких отрезков времени, должно быть целое число N (время между любыми последовательными моментами совпадения стрелок постоянно). Таким образом, запишем: 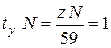 . Отсюда получим
. Отсюда получим 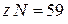 , но поскольку 59 простое число, то
, но поскольку 59 простое число, то 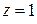 и
и 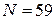 , а число “выступлений” кукушки за час равно N + 1 = 60. Учитывая, что в сутках 24 часа, найдём количество “просыпаний” кукушки за полные сутки: Nсутки = 1 + N , 24 =
, а число “выступлений” кукушки за час равно N + 1 = 60. Учитывая, что в сутках 24 часа, найдём количество “просыпаний” кукушки за полные сутки: Nсутки = 1 + N , 24 =

1 + 59 , 24 = 1417 раз.
Задача № 4 ( 10 баллов ) Решение: (РОФ, 2007)
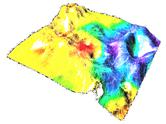
Если в результирующая сила, направленная по касательной к траектории движения спортсменов, после прохождения им центра ямы будет пропорциональна пройденному пути, отсчитываемому по дуге снизу вверх (то есть 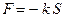 ), то уравнение движения сноубордиста будет иметь вид
), то уравнение движения сноубордиста будет иметь вид 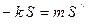 . Решение этого уравнения с учётом начальных условий имеет вид S (t) = S 0 sin ω t, причём независимо от начальной амплитуды S 0, как и требуется по условию данной задачи. Тогда получим:
. Решение этого уравнения с учётом начальных условий имеет вид S (t) = S 0 sin ω t, причём независимо от начальной амплитуды S 0, как и требуется по условию данной задачи. Тогда получим:
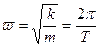 = Const (1).
= Const (1).
С другой стороны, выражению для силы 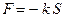 соответствует выражение для потенциальной энергии
соответствует выражение для потенциальной энергии 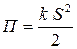 (2).
(2).
Однако помимо этого, гравитационная потенциальная энергия может быть выражена и через вертикальную координату Y. Тогда получим: 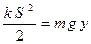 или
или 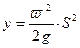 (3) или
(3) или 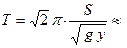 20c. Отсюда определим время спуска равное
20c. Отсюда определим время спуска равное 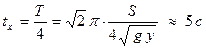 (4).
(4).
Так как dS2 = dx2 + dy2, то: 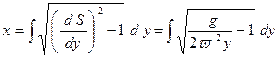 (5).
(5).
Интегрирование удобнее всего провести, сделав подстановку
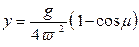 Тогда получим:
Тогда получим: 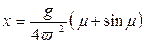 (6).
(6).
Эти уравнения задают в параметрическом виде уравнение циклоиды.
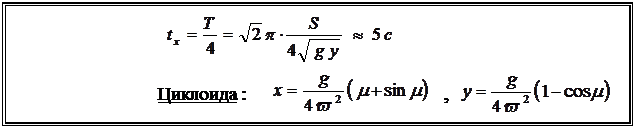

ОТВЕТ:
Задача № 5 ( 4 балла ) Решение: (РТ ОФШ 10кл, 2005)
 |
Прейдём в систему отсчёта, в которой поезд неподвижен. В такой системе отсчёта пассажир бежит с постоянным ускорением, а к “хвосту” поезда, то есть в сторону увеличения номеров вагонов. Его перемещения до начала и конца вагона под номером m равны, соответственно:
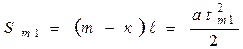 (1) и
(1) и 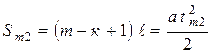 (2).
(2).
Такие же выражения запишем для определения перемещения к вагону под номером n.
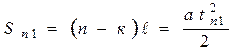 (3) и
(3) и 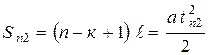 (4).
(4).
Из (1) – (4) получим: 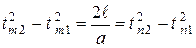 или, исключая
или, исключая 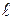 и a
и a 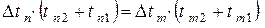 (5).
(5).
По условию: 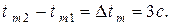 (6).
(6).
Из (5) – (6) найдём искомое время прохождения мимо пассажира вагона под номером n:
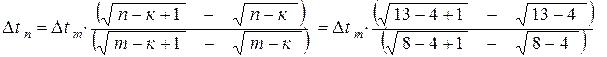 (7).
(7).
Окончательно получим:
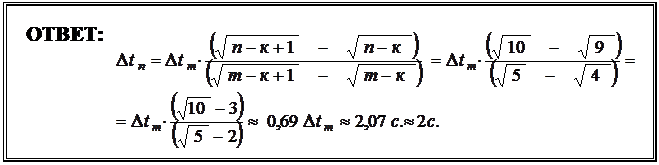
Задача № 6 ( 6 баллов ) Решение: (РОФ, 2010)

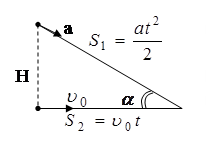
Перейдём в систему отсчёта, в которой Карлсон сначала неподвижно висит в воздухе. В этой системе отсчёта банка варенья движется с постоянной скоростью  ( прямо из-под висящего над ней на высоте h Карлсона) в каком-то направлении по горизонтальной прямой. Очевидно, что в такой системе отсчёта любитель варенья должен двигаться по прямой с максимальным ускорением a. При этом время, за которое он достигнет банки равно времени движения самой банки. Из этих рассуждений и теоремы Пифагора (см. рисунок) следует:
( прямо из-под висящего над ней на высоте h Карлсона) в каком-то направлении по горизонтальной прямой. Очевидно, что в такой системе отсчёта любитель варенья должен двигаться по прямой с максимальным ускорением a. При этом время, за которое он достигнет банки равно времени движения самой банки. Из этих рассуждений и теоремы Пифагора (см. рисунок) следует:
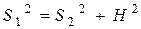 или
или 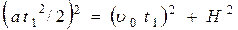 (1).
(1).
Отсюда определим искомое минимальное время, необходимое Карлсону для того, чтобы добраться до варенья.
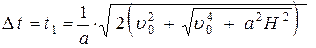 (2).
(2).
При этом в вертикальной плоскости ускорение должно быть направлено под постоянным углом к горизонту равным
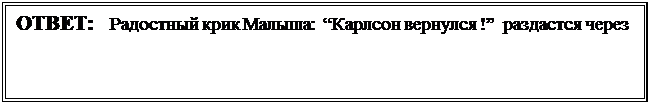
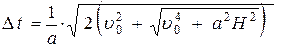
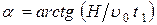 (3).
(3).
Задача № 7 ( 4 балла ) Решение: (ОФ, 2007)
Запишем для пройденного пути dS: d S = 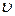 d t. Отсюда получим
d t. Отсюда получим
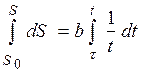 или
или 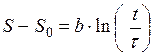 (1).
(1).
Для моментов времени t1 = 1час, t2 = 2 часа и t3 = 3 часа – запишем соответственно:
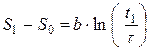 (2),
(2), 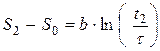 (3) и
(3) и 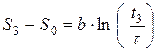 (4).
(4).
Исключая из (2) - (4) неизвестные a, S 0 и τ, получим:
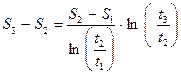 = (500-300) ln
= (500-300) ln 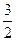 / ln
/ ln 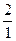 м = 117 м.
м = 117 м.
 |
Задача № 8 ( 4 балла ) Решение: (ОФ, 2006)
Уравнение параболы имеет вид y = ax – bx2, где параметры a и b равны соответственно: a = tg α (1), b = g (1+tg2 α) /2υ0 2 (2).
Тогда y 1 = a1 x 1– b1 x 12 (3), а также y 2 = a2 x 2– b2 x 2 2 (4).
Таким образом, поскольку y 1 = y 2 и x 1 = x 2, то:
0 = (а 1 - a 2) x 1 – (b 1 - b 2) x 1 2 или x 1 = S = (а 1 - a 2) / (b 1 - b 2) (5)
или S = 2υ0 2 (tg α 1 - tg α 2) / (tg2 α 1 - tg2 α 2)g.
Отсюда получим: S = 2υ0 2 / (tg α 1 + tg α 2)g = υ0 2 / g (6)

Ответ: 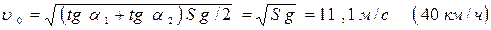
Задача № 9 (3 балла ) Решение: (РТ ОФШ 10кл, 2006)
 Из-за торможения в разряженной атмосфере радиус орбиты спутника действительно немного уменьшается. Вследствие этого, если бы он продолжал двигаться по круговой орбите её радиус должен был бы увеличиться. В реальности, после снижения скорости круговая орбита будет трансформироваться в эллиптическую орбиту, как показано на рисунке.
Из-за торможения в разряженной атмосфере радиус орбиты спутника действительно немного уменьшается. Вследствие этого, если бы он продолжал двигаться по круговой орбите её радиус должен был бы увеличиться. В реальности, после снижения скорости круговая орбита будет трансформироваться в эллиптическую орбиту, как показано на рисунке.
Из закона сохранения момента импульса для системы “спутник- Земля” получим 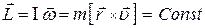 . Отсюда видно, что в верхней точке траектории движения на рисунке скорость наименьшая.
. Отсюда видно, что в верхней точке траектории движения на рисунке скорость наименьшая.
 Тот факт, что после торможения в атмосфере скорость движения спутника не уменьшается, а возрастает- удивляет. Однако, если присмотреться поближе к рассматриваемому вопросу, станет понятно, что это нисколько не противоречит закону сохранения энергии. Попробуем разобраться - почему это так. Относительно инерциальной системы отсчёта, жёстко связанной с Землёй, на спутник во время его полёта действует несколько сил, из которых основные: сила тяготения и сила сопротивления при движении в разряженном воздухе.
Тот факт, что после торможения в атмосфере скорость движения спутника не уменьшается, а возрастает- удивляет. Однако, если присмотреться поближе к рассматриваемому вопросу, станет понятно, что это нисколько не противоречит закону сохранения энергии. Попробуем разобраться - почему это так. Относительно инерциальной системы отсчёта, жёстко связанной с Землёй, на спутник во время его полёта действует несколько сил, из которых основные: сила тяготения и сила сопротивления при движении в разряженном воздухе.

Так как гравитационная сила притяжения к нашей планете имеет радиальный характер, то эта сила не может менять касательную (тангенциальную) по отношению к круговой орбите спутника составляющую скорости его движения. Именно эту составляющую скорости и уменьшает сила сопротивления, появляющаяся при движении в атмосфере. Однако, в радиальном направлении на тело действует сила тяжести, безусловно, разгоняя любое тело и увеличивая его скорость по направлению к центру планеты. Таким образом, понятно, что в целом значение полной скорости 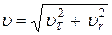 со временем будет возрастать, даже при сильном уменьшении горизонтальной составляющей скорости. Эти рассуждения не противоречат закону сохранения энергии, согласно которому убыль гравитационной потенциальной энергии расходуется на увеличение кинетической энергии спутника в радиальном направлении.
со временем будет возрастать, даже при сильном уменьшении горизонтальной составляющей скорости. Эти рассуждения не противоречат закону сохранения энергии, согласно которому убыль гравитационной потенциальной энергии расходуется на увеличение кинетической энергии спутника в радиальном направлении.
Задача № 10 (4 балла ) Решение: (ОФ, 2004)
Так как движение мяча вдоль оси x на первом участке (t 1) на втором участке траектории (t 2) является равномерным (т.к. вдоль оси x не действуют силы, а при этом скорость движения по горизонтали постоянна и равна начальной скорости вдоль оси x: 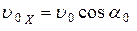 ), то:
), то:
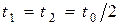 (1) (время движения мяча равно
(1) (время движения мяча равно 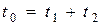 )
)
Движение мяча по оси y равнозамедленное (a = - g) с начальной скоростью 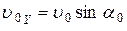 . Запишем для первого и второго участка траектории:
. Запишем для первого и второго участка траектории:
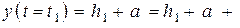
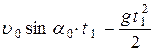 (2)
(2)
и 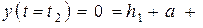
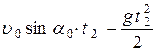 (3).
(3).
Складывая (2) и (3), получим: 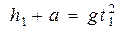 (4) или
(4) или 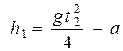 = 2,32 м. (рост Увáйса).
= 2,32 м. (рост Увáйса).
Отсюда определим и 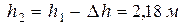 (рост Яниса). Тогда высота, на которой расположено баскетбольное кольцо, равна
(рост Яниса). Тогда высота, на которой расположено баскетбольное кольцо, равна 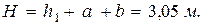
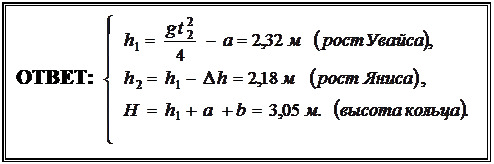
Задача № 11 (8 баллов ) Решение: (РОФ, 2006)
Масса воды в струе m = ρ·V, где V = L·S - объем струи в воздухе, S – площадь сечения струи, L – длина параболы.
Рассмотрим данную задачу при условии полного отсутствия гравитации. В этом случае - длина параболы L была бы равна длине струи, которая летит равномерно со скоростью υ0. L = υ0·t1
Время полета струи t1 найдем из уравнения изменения координаты y для параболы, по которой летит вода под действием силы притяжения к земле.
y = y0 +υ0 sin α . t - 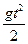 . Здесьy0 = 0, y1 = y (t = t1) = h (1).
. Здесьy0 = 0, y1 = y (t = t1) = h (1).
Таким образом, получим: 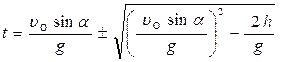 (2) или, так как вода на крышу падает сверху, то из двух возможных значений времени выбираем бóльшее. Отсюда найдём:
(2) или, так как вода на крышу падает сверху, то из двух возможных значений времени выбираем бóльшее. Отсюда найдём: 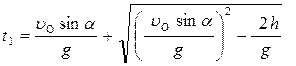 (3),
(3),
тогда искомая масса воды равна m = ρ S υ0.

Задача № 12 ( 4 балла ) Решение: (РТ ОФШ 11 кл, 2005)
Запишем в координатах x, y уравнение параболы, проходящей через точку А, расположенную на высоте H+h над яблоком:
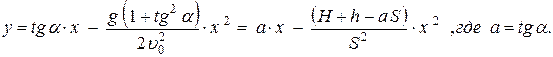 (1)
(1)
Так как при этом 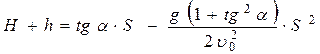 , то получим:
, то получим:
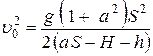 (2). Для постоянных H и h определим значение
(2). Для постоянных H и h определим значение 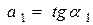 соответствующее наименьшему значению начальной скорости броска, приравняв производную от
соответствующее наименьшему значению начальной скорости броска, приравняв производную от 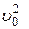 по a к нулю. В результате получим:
по a к нулю. В результате получим:
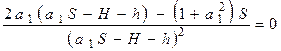 или
или 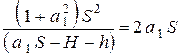 (2)
(2)
Решив данное квадратное уравнение 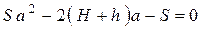 , найдём
, найдём 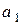 :
:
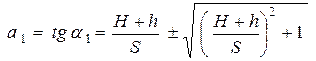 или, с учётом того, что
или, с учётом того, что 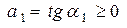 ,
,
запишем: 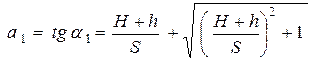 (3)
(3)
Соответствующая этому углу минимальная скорость 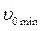 , с учётом (2), равна:
, с учётом (2), равна:
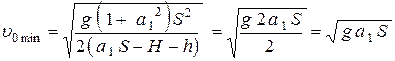 (4)
(4)
Из (4) видно, что скорость минимальна при наименьшем угле броска, а следовательно при h равном нулю. Таким образом доказано, что траектория должна проходить через точку А- яблоко, при этом:
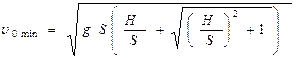 (5)
(5) 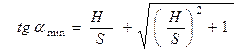 (6)
(6)
P. S. Эти же результаты можно получить другим способом. Запишем пройденный стрелой путь по горизонтальной и вертикальной осям - S и H:
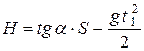 (7) и
(7) и 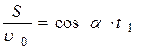 (8).
(8).
Будем искать максимум функции 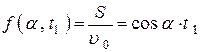 при условии, что
при условии, что 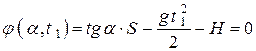 . Другими словами, будем искать условный экстремум. Для нахождения критических точек, только среди которых могут находиться точки экстремума, необходимо рассмотреть функцию
. Другими словами, будем искать условный экстремум. Для нахождения критических точек, только среди которых могут находиться точки экстремума, необходимо рассмотреть функцию 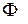 , называемую функцией Лагранжа, которая равна:
, называемую функцией Лагранжа, которая равна:
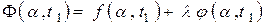 (9).
(9).
Построим функцию Лагранжа:
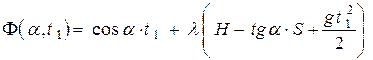 (10).
(10).
Так как критические точки функции определяются условиями:
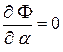 ,
, 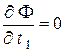 и
и 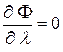 (11),
(11),
то получим систему из трёх уравнений.
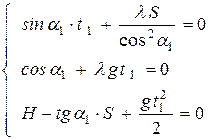 или
или 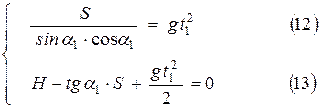
Из (12) и (13) получим: 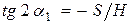 или
или 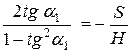 (14),
(14),
или 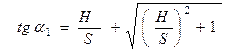 , что совпадает с первым решением. Из (13)
, что совпадает с первым решением. Из (13)
определим и время полёта стрелы: 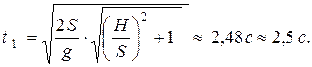

Ответ 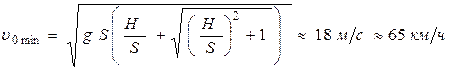
Задача № 13 (6 баллов ) Решение: (РОФ, 2009)
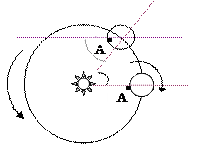 Из рисунка видно, что, если нет собственного вращения планеты, то во время движения Венеры по орбите любая неподвижная точка на её поверхности (например точка А) поворачивается в направлении противоположном орбитальному вращению планеты (см. рис.).
Из рисунка видно, что, если нет собственного вращения планеты, то во время движения Венеры по орбите любая неподвижная точка на её поверхности (например точка А) поворачивается в направлении противоположном орбитальному вращению планеты (см. рис.).
В реальности Венера обладает собственным вращением в этом же направлении. Её общая угловая скорость равна: ωобщ = ωорбит + ωсобств или так как ω = 2π / T,то равенство примет вид:
1/Tобщ = 1/ Tорбит+1/ Tсобств, 1/Tобщ = 1/T1 + 1/ T2 или Tночь= Tобщ /2 = 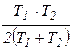 .
.

Ответ: Tночь= Tобщ /2 = 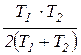 = 58,4 суток ≈ 2 мес.
= 58,4 суток ≈ 2 мес.
Задача № 14 (6 баллов ) Решение: (РОФ, 2009)
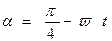
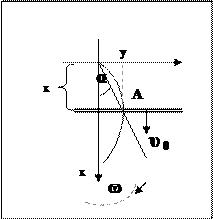 Так как секундная стрелка движется с постоянной угловой скоростью ω =
Так как секундная стрелка движется с постоянной угловой скоростью ω = 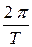 (T = 60 c), то
(T = 60 c), то
Угол поворота стрелки равен:., при этом координаты точки A - точки пересечения
движущейся со скоростью υ 0 считывающей линейки сканера и секундной стрелки, определяются системой двух уравнений:
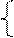 x (t) = υ 0 t, y (t) = x tg (
x (t) = υ 0 t, y (t) = x tg (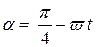 ).
).
или в декартовых и полярных координатах: 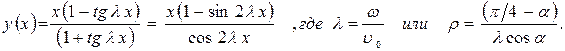
Исключая время, запишем искомое уравнение движения точки А в виде:
yА(x) = x А tg (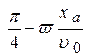 ). Отсюда при x А = b и y А = 0 получим:
). Отсюда при x А = b и y А = 0 получим:
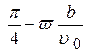 = 0 или
= 0 или 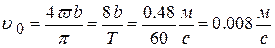 . Время, затраченное на сканирование сказки равно по условию t = 123,45 .
. Время, затраченное на сканирование сказки равно по условию t = 123,45 . 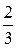 мин = 82,3 мин = 4938 с. Для N страниц длиной L = 297 мм каждая получим:
мин = 82,3 мин = 4938 с. Для N страниц длиной L = 297 мм каждая получим:  =
= 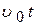 . Окончательно получим, что число страниц в книге равно
. Окончательно получим, что число страниц в книге равно 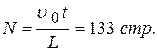

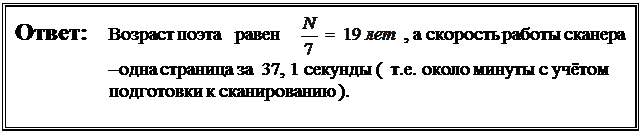
Задача № 15 (4 балла ) Решение: (РОФ, 2000)
При вращении планет вокруг общего центра масс- Солнца для них выполняется 3-й закон Кеплера:
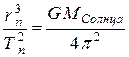 (1).
(1).
В частности, для Земли запишем: 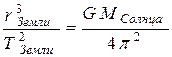 (2).
(2).
В том случае, когда траектория движения планеты – окружность, данный закон легко выводится из условия равенства гравитационной силы притяжения и центробежной силы инерции.
Отметим, однако, что третий закон Кеплера (который был опубликован им в 1609г.- через 16! лет после начала своих исследований) на самом деле неточен, что позже показал Ньютон, обосновав уточнённый 3-й закон Кеплера: 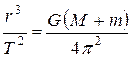 . Тогда из (1) следует соотношение:
. Тогда из (1) следует соотношение: 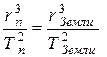 (3) или
(3) или 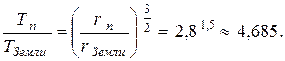 Отсюда найдём продолжительность одного года на Фаэтоне -
Отсюда найдём продолжительность одного года на Фаэтоне - 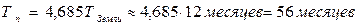
 |
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 645; Нарушение авторских прав?; Мы поможем в написании вашей работы!