
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вращение твёрдого тела. Юла, если на неё смотреть сверху, будет прецессировать против часовой стрелки, так как момент сил трения
|
|
|
|
Задача № 23 (2 балла) Решение: (ОФ, 2010)
Юла, если на неё смотреть сверху, будет прецессировать против часовой стрелки, так как момент сил трения, возникающий в месте соприкосновения оси юлы с поверхностью и действующий на ось, направлен вниз.После того, как вращение юлы замедлится, она коснётся боком горизонтальной поверхности, что приведёт к изменению вращения оси юлы на противоположное так как, вектор момента сил трения повернётся на 180 0.
К тем же выводам мы придём, если воспользуемся законом сохранения момента импульса 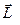 (в проекциях на вертикальную ось): полный момент импульса замкнутой системы (по 3-му закону Ньютона силы, действующие внутри системы “поверхность и юла “ равны и противоположны, а проекция момента силы тяжести на вертикальную ось равна нулю) не изменяется со временем. Таким образом, в любой момент времени полный момент импульса системы равен первоначальному, то есть в данном случае – нулю. Тогда запишем:
(в проекциях на вертикальную ось): полный момент импульса замкнутой системы (по 3-му закону Ньютона силы, действующие внутри системы “поверхность и юла “ равны и противоположны, а проекция момента силы тяжести на вертикальную ось равна нулю) не изменяется со временем. Таким образом, в любой момент времени полный момент импульса системы равен первоначальному, то есть в данном случае – нулю. Тогда запишем:  .
.
Отсюда видно, что угловые скорости вращения юлы вокруг собственной оси и вокруг вертикальной оси, в проекциях на эту ось, всегда противоположны.
Задача № 24 (6 баллов) Решение: (ОФ, 2009)

После того, как масса Земли станет равной массе Солнца, она будет вращаться вокруг их общего центра масс (точка B), при этом расстояние между ними не изменится, а новой траекторией движения будет окружность радиусом  .
.
Приравнивая в первом и во втором случае центробежную силу инерции и и силу гравитационного притяжения, получим:
 (1) и
(1) и  (2).
(2).
Разделив левые и правые части уравнений, найдём:
 |
 или
или  или
или 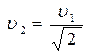 (3). Время, за которое совершается один оборот (Т- период) равно
(3). Время, за которое совершается один оборот (Т- период) равно 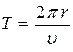 . Отсюда получим:
. Отсюда получим: 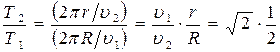 . Так как T1 = 12 месяцев, то новый год будет длиться 8,5 месяцев, а новое лето- 2 месяца и 4,7дня.
. Так как T1 = 12 месяцев, то новый год будет длиться 8,5 месяцев, а новое лето- 2 месяца и 4,7дня.
Задача № 25 (7 баллов) Решение: (ОФ ИПИ, 1988)
Рассмотрим сначала просто держащегося за нить муравья. В этом случае имеем два уравнения, вытекающих соответственно из 2-го закона Ньютона-  и основного закона динамики вращения твёрдого тела-
и основного закона динамики вращения твёрдого тела- 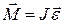 :
:
 (1) и
(1) и 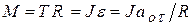 или
или 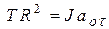 (2). Отсюда, исключая Т, найдём тангенциальное ускорение нити, совпадающее с ускорением движения груза вниз:
(2). Отсюда, исключая Т, найдём тангенциальное ускорение нити, совпадающее с ускорением движения груза вниз: 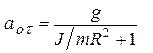 (3). Сила натяжения нити при этом равна:
(3). Сила натяжения нити при этом равна:
 (4).
(4).
Если муравей побежит вверх с ускорением a относительно нити, то (в системе отсчёта, движущейся вместе с ним) на нить дополнительно к силе тяжести будет действовать направленная вниз сила инерции 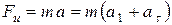 (здесь через
(здесь через 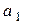 обозначено ускорение муравья относительно пола). При этом тангенциальное ускорение нити будет по-прежнему определяться уравнением (3), при условии, что напряжённость гравитационного поля Земли возросла до значения
обозначено ускорение муравья относительно пола). При этом тангенциальное ускорение нити будет по-прежнему определяться уравнением (3), при условии, что напряжённость гравитационного поля Земли возросла до значения 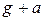 . Тогда найдём:
. Тогда найдём:
 (5), и
(5), и  (6).
(6).
Учитывая, что ускорение муравья относительно нити 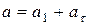 (7),
(7),
и отсюда 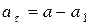 (8), получим из (5):
(8), получим из (5):  (8).
(8).
Выражая отсюда ускорение относительно пола 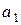 , найдём:
, найдём:
 (9), при этом
(9), при этом  (10).
(10).
Поскольку относительное ускорение по второму закону Ньютона равно  (11), то получим:
(11), то получим:
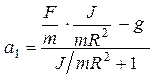 (12),
(12), 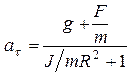 (13) и
(13) и  (14).
(14).
К этим же результатам можно прийти, если перейти в неинерциальную систему отсчёта, в которой нить неподвижна. В этом случае уравнения движения системы будут иметь вид:
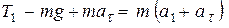 и
и  , где
, где  .
.
Из (12) следует, что при движении муравья вверх (относительно пола)
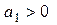 или
или  . Если
. Если  (15), то муравей поднимается вверх с постоянной скоростью, при этом
(15), то муравей поднимается вверх с постоянной скоростью, при этом 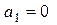 . Так как момент инерции катушки в соответствии с условием задачи равен
. Так как момент инерции катушки в соответствии с условием задачи равен 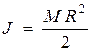 , то получим
, то получим  , где P - вес муравья.
, где P - вес муравья.
Отсюда найдём- при массе катушки  муравей поднимается вверх. Так как значение силы, действующей со стороны насекомого на нить, изменяется в диапазоне значений от нуля до указанного в условиях задачи максимального значения F, то для движения вверх -
муравей поднимается вверх. Так как значение силы, действующей со стороны насекомого на нить, изменяется в диапазоне значений от нуля до указанного в условиях задачи максимального значения F, то для движения вверх - 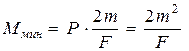 .
.
 |
Задача № 26 (6 баллов ) Решение: (РОФ, 2006)

Несложно доказать, что центр масс тела должен находится на прямой, проходящей через центры масс “половинок” спортсмена. Одновременно с этим, он должен принадлежать вертикальной прямой, проходящей через точку подвеса, так как центр масс спортсмена (т.C) не может сместиться вдоль горизонтальной оси (F x = 0). Таким образом, ясно, что точка C на рисунке находится в центре правого нижнего квадрата.
Тогда из Δ АBС получим:
 |
tg β = |СB| / |AB| = (L/4) / (L/2+ L/4) = 1/3.
Задача № 27 (6 баллов ) Решение: (РОФ, 2004)

Из рисунка видно, что камень, имеющий форму куба, может начать перекатываться по дну реки (поворот вокруг точки А) при условии, что:
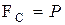 (1), (при этом вращающие моменты силы тяжести и силы сопротивления равны друг другу-
(1), (при этом вращающие моменты силы тяжести и силы сопротивления равны друг другу-  ).
).
По условию: 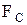 ~
~ 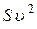 (2). Тогда из (1) и (2) следует, что
(2). Тогда из (1) и (2) следует, что  ~
~  (3). Если учесть, что при этом вес камня пропорционален кубу его размера
(3). Если учесть, что при этом вес камня пропорционален кубу его размера 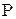 ~
~  (4), а площадь его поперечного сечения прямо пропорциональна квадрату его размера
(4), а площадь его поперечного сечения прямо пропорциональна квадрату его размера 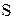 ~
~ 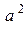 (5), то получим:
(5), то получим:
 ~
~ 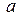 (6). С учётом (3) найдём:
(6). С учётом (3) найдём:  ~
~  (7). Данная пропорция показывает, что если поток воды имеет скорость
(7). Данная пропорция показывает, что если поток воды имеет скорость 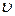 , то минимальный размер камней, переворачиваемых им, зависит от квадрата его скорости.
, то минимальный размер камней, переворачиваемых им, зависит от квадрата его скорости.
Поскольку, в соответствии с выражением (4), вес камня  пропорционален кубу его характерного размера, то получим утверждение, которое в гидрологии носит название “закон Эри”:
пропорционален кубу его характерного размера, то получим утверждение, которое в гидрологии носит название “закон Эри”:  ~
~ 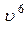 (т.е. “увеличение скорости течения в
(т.е. “увеличение скорости течения в  раз сообщает потоку способность увлекать предметы в
раз сообщает потоку способность увлекать предметы в  раз более тяжёлые ”.
раз более тяжёлые ”.
Окончательно получим: 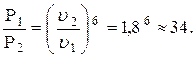
 |
Задача № 28 (7 баллов ) Решение: (РОФ, 2005)

При движении по дуге окружности тело будет иметь нормальное ускорение под действием силы реакции опоры со стороны стенки и тангенциальное ускорение под действием силы трения:
ma n = N, (1)
ma t = - F тр, (2) и F тр = kN. (3)
Решая совместно уравнения (1), (2), (3), получим:
 - a t = ka n, или
- a t = ka n, или  . (4)
. (4)
Так как  , то
, то  .
.
Подставим последнее выражение в (4), получим:
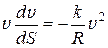 ,
,  .
.

Интегрируя, получим:  или
или 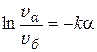 или = 1/3.
или = 1/3.
Задача № 29 (6 баллов ) Решение: (РОФ, 2010)

 1-й способ: По теореме, связывающей для плоской пластины моменты инерции I1 и I2 относительно любых двух взаимно перпендикулярных осей, лежащих в её плоскости, с моментом инерции I3 относительно оси, проходящей через пересечение первых двух и перпендикулярной плоскости пластины, запишем следующее равенство:
1-й способ: По теореме, связывающей для плоской пластины моменты инерции I1 и I2 относительно любых двух взаимно перпендикулярных осей, лежащих в её плоскости, с моментом инерции I3 относительно оси, проходящей через пересечение первых двух и перпендикулярной плоскости пластины, запишем следующее равенство:
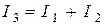 (1).
(1).
Отсюда, так как  и
и  , то
, то  (2).
(2).
Так как при любом угле поворота  , а
, а  не изменяется, то не зависят от угла и значения моментов инерции I1 и I2 .
не изменяется, то не зависят от угла и значения моментов инерции I1 и I2 .
2-й способ:
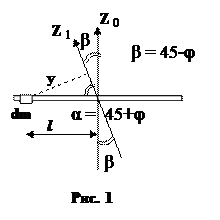
Из рисунка 1 видно (так как I 0 - момент инерции стержня относительно оси z0 равен 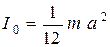 и поскольку
и поскольку  ),что момент инерции относительно оси z 1 равен:
),что момент инерции относительно оси z 1 равен:
 (1), где a - длина стержня. Тогда для бесконечно тонкого стержня:
(1), где a - длина стержня. Тогда для бесконечно тонкого стержня:
 (2).
(2).
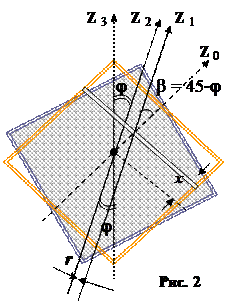 Рассматривая квадратную пластину как бесконечный набор таких стержней, определим её момент инерции-
Рассматривая квадратную пластину как бесконечный набор таких стержней, определим её момент инерции-  .
.
С учётом формулы (2) и теоремы Штейнера найдём момент инерции тонкого стержня длиной
a (светлая полоска на рисунке 2) относительно
оси z2:
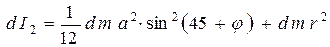 (3),
(3),
где 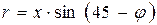 , а x – смещение данной полосы от центра квадрата.
, а x – смещение данной полосы от центра квадрата.
Заменив массу бесконечно тонкого стержня на
 и интегрируя по координате x от
и интегрируя по координате x от  до
до  , получим следующее
, получим следующее
выражение:
 (4).
(4).
После интегрирования и упрощений получим:
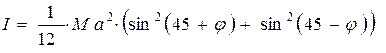 (5).
(5).
Интересно отметить, что выполняются следующие тригонометрические тождества:
 и
и 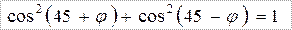
Таким образом, прямым расчётом также приходим к выводу, что момент инерции квадратной пластины относительно любой оси, лежащей в плоскости пластины и проходящей через её центр, имеет одно и то же значение

 .
.
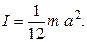
Задача № 30 (6 баллов ) Решение: (РОФ, 2009)
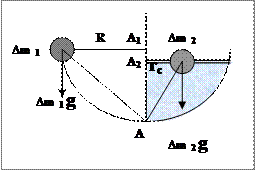
Моменты сил, действующих на центр масс полукруглой тонкой пластины (верхний слой жидкости толщиной ∆h) и необходимый для возврата равновесия дополнительный груз ∆m 2 = ρ π r2 ∆h / 2, равны относительно т.А, (либо т. А1 или т. А2, так как они смещены вверх относительно т.А параллельно равнодействующей силе):
Тогда запишем:  или
или 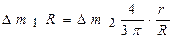
Учитывая, что 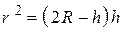 , а так же, что
, а так же, что 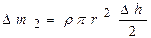 , получим:
, получим:
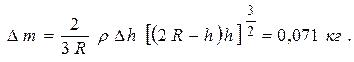
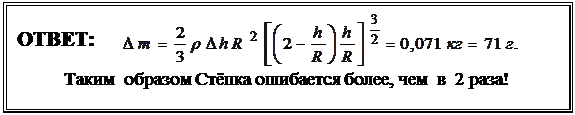
Задача № 31 (6 баллов ) Решение: (РОФ, 2003)
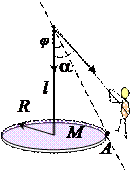 На диск, в момент начала его переворачивания- вращения вокруг точки А в вертикальной плоскости- действуют два момента сил: момент силы тяжести
На диск, в момент начала его переворачивания- вращения вокруг точки А в вертикальной плоскости- действуют два момента сил: момент силы тяжести 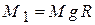 и момент силы упругости
и момент силы упругости  . Для того, чтобы диск начал переворачиваться, значение момента силы упругости должно сравнятся со значением удерживающего от поворота вокруг точки А момента силы тяжести. Таким образом, можем записать:
. Для того, чтобы диск начал переворачиваться, значение момента силы упругости должно сравнятся со значением удерживающего от поворота вокруг точки А момента силы тяжести. Таким образом, можем записать:  или
или 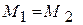 или
или
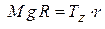 (1). С учётом, того, что
(1). С учётом, того, что  , получим:
, получим:
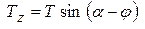 (2) или
(2) или  .
.
Упрощая полученное выражение и подставляя значения 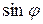 и
и 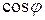 ,
,
получим: 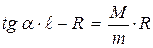 (3), так как
(3), так как  и
и 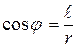 .
.
Отсюда найдём: 
 (4) или
(4) или 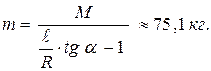
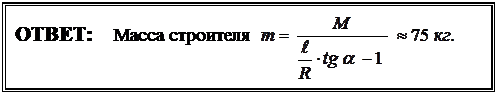
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 702; Нарушение авторских прав?; Мы поможем в написании вашей работы!