
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы сохранения в механике
|
|
|
|
Задача № 32 (4 балла) Решение: (ОФ, 2001)
 Вес тела по определению есть, сила давления на опору. В данном случае реакция опоры возникает под действием тормозящей упругой силы и силы тяжести и расположена под углом к горизонту по ходу движения самолёта в направлении противоположном суммарной силе, действующей на самолёт.
Вес тела по определению есть, сила давления на опору. В данном случае реакция опоры возникает под действием тормозящей упругой силы и силы тяжести и расположена под углом к горизонту по ходу движения самолёта в направлении противоположном суммарной силе, действующей на самолёт.
Таким образом, вес пилота с  возрастает до значения:
возрастает до значения:
 (1).
(1).
Ускорение самолёта определим из формулы, связывающей пройденный путь при равнопеременном движении с ускорением и значениями начальной и конечной скоростей: 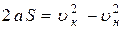 (2). Так как
(2). Так как 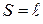 , а
, а  и
и  ,
,
то ускорение  равно
равно 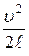 .
.
Величина перегрузки, испытываемая пилотом, равна при этом: 


Задача № 33 (7 баллов ) Решение: (РОФ и РТ ОФШ 10 кл, 2006)
По закону сохранения импульса (считая, что при минимальной скорости игрушки она, поднявшись на горку, далее движется вместе с ней с такой же скоростью u), определим скорость u:  (1).
(1).
Кроме того, по закону сохранения энергии запишем:
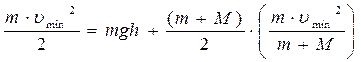 или
или 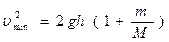 (2).
(2).
Тогда получим: υmin =  .
.
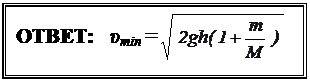
Задача № 34 (4 балла ) Решение: (ОФ ИПИ, 1986)
Во время движения обруча на него действуют три силы- сила тяжести, реакция опоры и сила трения скольжения (действием силы трения качения можно пренебречь). Сила тяжести и реакция опоры уравновешивают друг друга. Таким образом, фактически, движение обруча определяется действием силы трения скольжения равной Fтр = μ mg. Работа силы трения идёт на уменьшение скорости движения при поступательном движении (А1) и, кроме того, она обеспечивает замедление вращения обруча (А2). Полная работа силы трения скольжения при этом равна А = А1 + А2 = Q, где Q – количество теплоты, полученное как поверхностью- Q1, так и самим обручем- Q2 в результате действия силы трения. С учётом III- го закона Ньютона ясно, что Q1 и Q2 равны.
 , где
, где 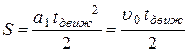 (1)
(1)
 (2)
(2)
Отметим также, что  (поскольку при а1 = Const, 2а1 S =
(поскольку при а1 = Const, 2а1 S =  )
)
При записи уравнений (1) и (2) учтено, что и поступательное и вращательное движение обруча равнозамедленное, так как сила трения скольжения постоянна. Следует заметить, что если тело имеет вид обруча, тангенциальное ускорение и ускорение при поступательном движении тела равны.
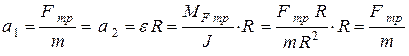
 (3)
(3)
Из (1) и (2) получим: 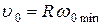 (4) или
(4) или  (5).
(5).
К такому же соотношению придём, рассматривая по отдельности поступательное и вращательное движение обруча. Запишем по теореме о связи работы силы и изменении кинетической энергии тела, движущегося под действием этой силы следующие уравнения:
 (6) и
(6) и  (7)
(7)
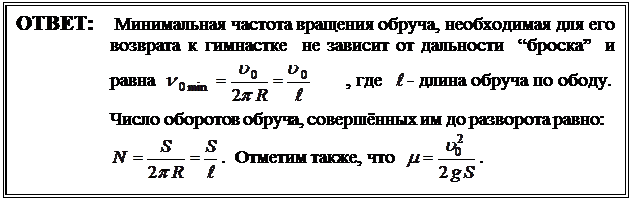 |
Задача № 35 (4 балла ) Решение: (РТ ОФШ 11 кл, 2007)
Найдёмсреднее давление, которое оказывает дождь на лобовое стекло автомобиля, движущегося с постоянной скоростью υ. Угол наклона стекла по отношению к дороге α равен 60 0. Можно считать, что капли дождя падают с постоянной скоростью u. Интенсивность дождя - h (мм)осадков в час.
В системе отсчёта, движущейся с постоянной скоростью вместе с автомобилем, капли падают на него под углом β к вертикали, причём 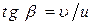 . Угол падения на лобовое стекло автомобиля при этом равен
. Угол падения на лобовое стекло автомобиля при этом равен  . Достаточно заметное влияние на процесс отражения капли от стекла оказывают эффекты смачивания и поверхностного натяжения воды. Это позволяет нам приближённо рассчитывать искомое давление в рамках модели, в которой удар капли о стекло является неупругим. Сила, определяющая давление, создаваемое одной каплей дождя, на лобовое стекло автомобиля по нормали к нему (ось z), равна:
. Достаточно заметное влияние на процесс отражения капли от стекла оказывают эффекты смачивания и поверхностного натяжения воды. Это позволяет нам приближённо рассчитывать искомое давление в рамках модели, в которой удар капли о стекло является неупругим. Сила, определяющая давление, создаваемое одной каплей дождя, на лобовое стекло автомобиля по нормали к нему (ось z), равна:
 или
или  (1). Обозначим через N количество капель, упавших на стекло за рассматриваемый отрезок времени t. Тогда искомое давление дождя на лобовое стекло, движущегося автомобиля равно:
(1). Обозначим через N количество капель, упавших на стекло за рассматриваемый отрезок времени t. Тогда искомое давление дождя на лобовое стекло, движущегося автомобиля равно:

 (2).
(2).
Как видно из рисунка, N определяется количеством капель в скошенной призме с площадью основания S и длиной L, где 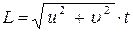 . Длина рассматриваемой призмы такова, что все содержащиеся в ней капли за время не более t достигают лобового стекла машины. С учётом вышесказанного определим N:
. Длина рассматриваемой призмы такова, что все содержащиеся в ней капли за время не более t достигают лобового стекла машины. С учётом вышесказанного определим N:  (3).
(3).
Таким образом, из (2) и (3) определим искомое давление:
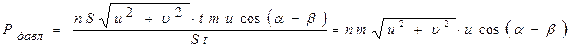 (4).
(4).
Найдём  -массу воды, в одном кубометре воздуха или, выражаясь образно, “плотность дождя”. За время tчас = 1 час на поверхности земли окажутся все капли из прямой призмы с площадью основания S1 и высотой
-массу воды, в одном кубометре воздуха или, выражаясь образно, “плотность дождя”. За время tчас = 1 час на поверхности земли окажутся все капли из прямой призмы с площадью основания S1 и высотой  .
.
М- масса воды в этой призме постоянна и равна массе слоя осадков. Следовательно, искомая “плотность дождя” определяется равенством:
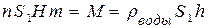 или
или  (5).
(5).
Из (4) и (5) окончательно получим:
 , где
, где
β = arctg (v/u).
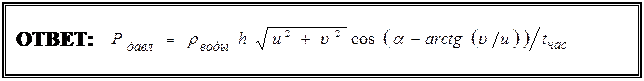 |
Задача № 36 (5 баллов ) Решение: (ОФ, 2005)
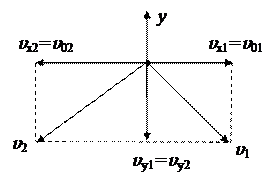
I –й способ:
По условию: v x1 = v 01 и v y1 = - gt,
v x2 = - v 02 и v y2 = - gt. Получим:
 и
и  .
.
Отсюда:  (1).
(1).
Решая совместно последние три равенства, получим:  (2).
(2).
Поскольку уравнения движения тел вдоль оси y одинаковы, расстояние между ними S = S x = (v x1+ v x2) t,  = 2,5 м.
= 2,5 м.
II –й способ:

По условию запишем: a1+ a2 = p/2,
или tg (p/2-a1) = tg a2; tg a1 × tg a2 = 1,
 или
или 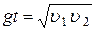 (1).
(1). 

Задача № 37 (5 баллов ) Решение: (ОФ, 2010)
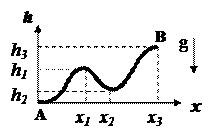 По условию задачи альпинист передвигает рюкзак медленно. Это означает, что в любой момент времени сумма действующих на рюкзак сил равна нулю. Рассматривая движение на небольшом участке длиной
По условию задачи альпинист передвигает рюкзак медленно. Это означает, что в любой момент времени сумма действующих на рюкзак сил равна нулю. Рассматривая движение на небольшом участке длиной  , расположенном под углом α к горизонтальной оси x, запишем для работы альпиниста на этом участке:
, расположенном под углом α к горизонтальной оси x, запишем для работы альпиниста на этом участке:  (1).
(1).
Здесь учтено, что при медленном перемещении груза  .
.
Так как  , получим:
, получим:  или поскольку
или поскольку  искомая работа равна:
искомая работа равна:

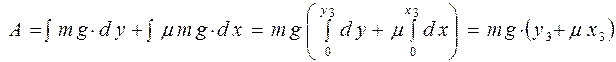
Задача № 38 (8 баллов ) Решение: (РОФ, 2008)
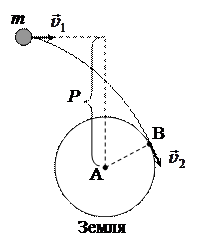
Рассмотрим такую начальную скорость v 1, при которой траектория астероида касается Земли. Применим закон сохранения момента импульса
(относительно точки А!):  .
.
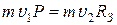 . Þ (1)
. Þ (1)
Если  <
<  , (2)
, (2)
то астероид упадет на Землю.
По закону сохранения энергии
 . (3)
. (3)
Решая совместно (2) и (3) получим ответ: катастрофа произойдет, если
 <
< 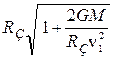 ,
,  <
<  ,
,  < 9008,5 км
< 9008,5 км
так как  , то катастрофа произойдет.
, то катастрофа произойдет.

Задача № 39 (7 баллов ) Решение: (РОФ, 2009)
 Космонавты перестанут видеть Землю, если гравитационное притяжение нашей планеты сможет “остановить ” свет, т.е. когда кванты электромагнитного излучения - фотоны не смогут преодолеть притяжение Земли. Очевидно, что необходимая для преодоления силы гравитационного притяжения кинетическая энергия частицы массы m должна быть не меньше, чем изменение при этом её потенциальной энергии.
Космонавты перестанут видеть Землю, если гравитационное притяжение нашей планеты сможет “остановить ” свет, т.е. когда кванты электромагнитного излучения - фотоны не смогут преодолеть притяжение Земли. Очевидно, что необходимая для преодоления силы гравитационного притяжения кинетическая энергия частицы массы m должна быть не меньше, чем изменение при этом её потенциальной энергии.
Тогда получим: 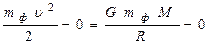 . Для того, чтобы фотон, перемещаясь со скоростью света, не смог бы покинуть поверхность планеты, необходимо выполнение условия
. Для того, чтобы фотон, перемещаясь со скоростью света, не смог бы покинуть поверхность планеты, необходимо выполнение условия 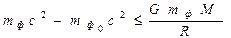 или
или 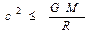 . Отсюда найдём искомый критический радиус сжатой под действием гравитации планеты:
. Отсюда найдём искомый критический радиус сжатой под действием гравитации планеты:  (1)
(1)
Таким образом, получим: при 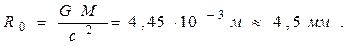
Другими словами, скорость света должна быть сопоставима с 1-й космической скоростью на поверхности “уменьшившейся ” планеты.
При более точном рассмотрении необходимо учесть высоту орбиты h, оценивая при этом в видимом диапазоне частот максимальную энергию фотона, как  , где
, где  - частота электромагнитного излучения, соответствующая фиолетовому свету.
- частота электромагнитного излучения, соответствующая фиолетовому свету.  (2), где
(2), где  и высота орбиты H определяется выражением, соответствующим 3-му закону Кеплера или являющимся следствием равенства центробежной силы инерции и гравитационной силы притяжения космической станции к планете:
и высота орбиты H определяется выражением, соответствующим 3-му закону Кеплера или являющимся следствием равенства центробежной силы инерции и гравитационной силы притяжения космической станции к планете:
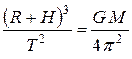 (3) или
(3) или 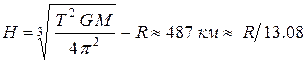 (4).
(4).
Получим:  . Отсюда, учитывая, что расстояние от центра планеты до станции постоянно (при этом
. Отсюда, учитывая, что расстояние от центра планеты до станции постоянно (при этом  ), найдём:
), найдём:
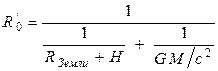 (5) или
(5) или 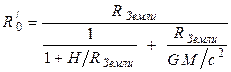 (6)
(6)
или 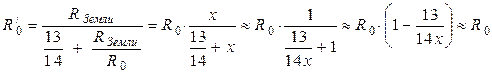 (7),
(7),
 где
где 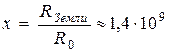
 |
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!