Колебания

Задача № 40 (5 баллов ) Решение: (РОФ, 2006)

Так как Т ~ Р^{A .} ρ^B. Е^C, то сравнивая размерности, получим: [с] = [Па] ^{A .} [ ] ^{B .}[ Дж] ^C или, поскольку [Па] = [ ] = [ ]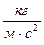, а [ Дж] = [ 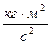], то: [c] = 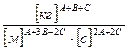и A+B+C = 0, A+3B- 2C = 0

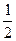и 2A+2C = -1. Решив систему, найдём: А= - , B= и C= .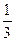

Тогда T= 1/ ν ~ 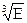или ν ~ 1/ 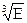. Отсюда получим:

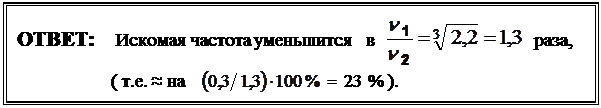
Задача № 41 (6 баллов ) Решение: (РОФ, 2003)

Определим сначала длины верёвок и :

Из треугольника ОАС найдём- 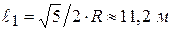и по теореме косинусов из треугольника ОВС, учитывая, что , получим-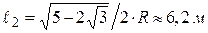

Также из ОВС найдём: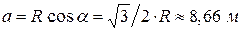

Заметим, что движение груза массы m на верёвках, есть вращение вокруг оси, проходящей через их точки крепления- А и В. Другими словами, система представляет собой “наклонный математический маятник”. Составляющая силы тяжести mg, направленная вдоль оси вращения, не влияет на колебания, а перпендикулярная составляющая- mg sin β является возвращающей силой по отношению к грузу. Таким образом, можно использовать формулу Гюйгенса для нахождения периода колебаний данного маятника только с эффективным значением ускорения свободного падения g*= g sin β:

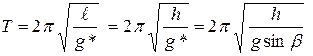(1).

Отсюда определим искомую частоту колебаний ν: ,

причём и 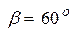. Обозначим углы: 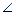ОАС через 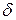, а 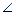ОАВ через 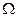. Тогда: ,

а 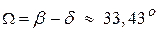. Отсюда найдём: , а следовательно, определим и искомую частоту.

Задача № 42 (9 баллов ) Решение: (РОФ, 2005)

Определим удлинение растяжки при наклоне трубы на малый угол a.

l ² = a ² + b ², (1)

(2)

,

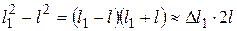Вычтем (2) из (1):

.

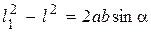Сравнивая два последних равенства и учитывая, что при малых углах sina @ a, получаем: (3)

На такую же величину сжимается вторая растяжка:

;

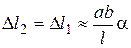, учитывая, что a = b = h /2 и ,

.

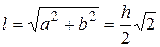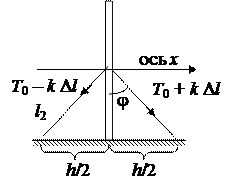
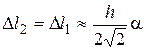Силы натяжения изменятся на величину (4)

Уравнение движения (вращения) трубы:

, где I = mh ²/3 – момент инерции трубы, М – суммарный момент сил натяжения и тяжести.

Момент сил натяжения равен:

. (5).

Момент сил тяжести равен: 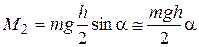(6).

Суммарный момент сил, действующий на трубу:

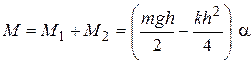. Преобразуем уравнение движения:

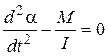, или, с учетом предыдущего выражения,

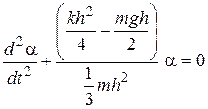, но , тогда

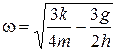, , или

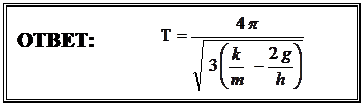Задача № 43 (3 баллов ) Решение: (ОФ, 2006)

Доска наиболее сильно раскачивается при резонансе. Тогда длина шага L будет равна длине волны, возникающей при упругих колебаниях доски, и период волны будет совпадать с собственным периодом упругих колебаний доски L = λ = υ·T (1), где T -собственный период колебаний доски, равный

T = 2π (2) (m – масса каскадера с доской и k - жесткость упругой доски).

Массу каскадера найдем из условия его равновесия, когда он неподвижен:

mg – kx₀= 0, где кх₀ – сила упругости, откуда: m= (3). Подставив

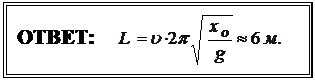выражение (3) в (2), затем (2) в (1), получаем: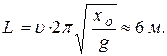

Задача № 44 (5 баллов ) Решение: (РОФ, 2002)

Докажем, что, если сосуд заполнен водой, то маятник можно считать математическим. Математическим можно считать маятник, у которого момент инерции равен I = m ℓ ², где ℓ- расстояние от точки подвеса до центра масс маятника. Относительно оси, проходящей через центр шара момент инерции воды равен нулю – она не вращается! Тогда для момента инерции маятника с незамёрзшей водой относительно точки подвеса по теореме Штейнера получим: I = m ℓ ². Таким образом – этот маятник действительно математический.

К такому же выводу мы придём, рассматривая изменения энергии маятника в задаче. Ясно, что кинетическая энергия поступательного движения маятника не убывает за счёт увеличения энергия вращения воды, что происходит в случае её замерзания, а как и в случае математического маятника возрастает только за счёт убыли потенциальной гравитационной энергии при его движении вниз. Следовательно, по формуле Гюйгенса период малых колебаний равен:

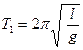( 1).

После замерзания воды маятник становится физическим: 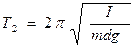(2).

Из равенств (1) и (2) получим:

;

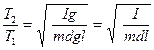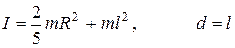
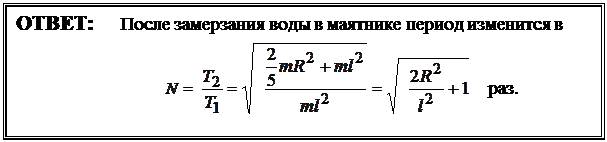
Задача № 45 ( 4 балла ) Решение: (РОФ, 1999)

Период колебаний золотых серёжек не изменится, если период колебаний добавленного груза будет таким же. Период колебаний физического маятника определяется выражением - (1), а период математического маятника - 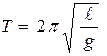(2).

В соответствии с условиями задачи имеем:

а) 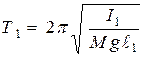- для физического маятника (квадратная пластина, подвешенная за одну из вершин и совершающая колебания в плоскости пластины). Здесь -момент инерции маятника, равный по теореме Штейнера:

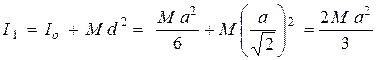(3), где 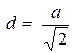и .

Тогда найдём: (4).

б) -для математического маятника (бриллиант или жемчужина, прикреплённые к вершине квадратной пластины на нити длиной ). Отсюда получим: (5).

Так как по условию задачи периоды и должны быть одинаковы, то:

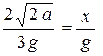или или:

, где . Отметим, что период колебаний, а значит и результат задачи не связан со значениями масс ни пластины, ни дополнительного груза.

Задача № 46 (5 баллов ) Решение: (ОФ ИПИ, 1987)

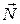Колебания шарика осуществляются в результате действия трёх сил: силы тяжести- , силы реакции опоры (сила упругости) и силы электрического взаимодействия за

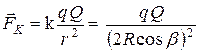рядов -силы Кулона, равной: (1). Поскольку 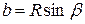и ,

то (2). Тогда для малых колебаний

() выражение для силы Кулона перепишется

в виде: (3). Определим проекцию на ось Z₂ результирующей силы 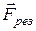, действующей на шарик по касательной: . Таким образом, при малых колебаниях на шарик вдоль оси x действует возвращающая сила 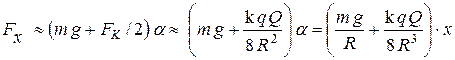или

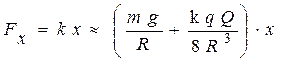(4).

Так как 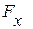линейно связана со смещением x, то малые колебания являются гармоническими с циклической частотой Отсюда, так как , то искомый период равен: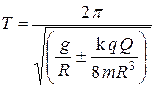

Глава II

Дата добавления: 2014-12-08