
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энтропия
|
|
|
|
Задача № 64 (6 баллов ) Решение: (ОФ, 2004)
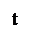
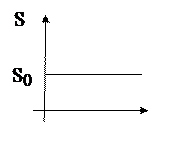 Так как
Так как 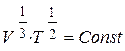 и
и 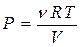 , то
, то 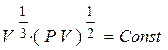 или
или 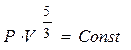 , но для одноатомного аргона это означает, что процесс, рассматриваемый в задаче, является адиабатическим, так как
, но для одноатомного аргона это означает, что процесс, рассматриваемый в задаче, является адиабатическим, так как  γ = 5/3 =
γ = 5/3 = 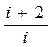 - показатель адиабаты.
- показатель адиабаты.
Таким образом, делаем вывод о том, что в данном процессе энтропия не изменяется S = Const, а искомый график имеет вид горизонтальной прямой.
 |
Задача № 65 (5 баллов ) Решение: (РОФ, 2002)
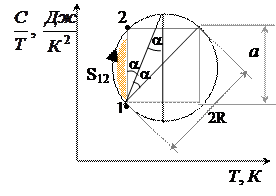
Так как 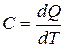 , а
, а 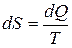 , то
, то 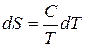 и
и 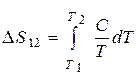 = S12 (1),
= S12 (1),
где S12 – площадь выделенного на рисунке сегмента окружности. Так как точки 1 и 2 принадлежат вписанному в окружность квадрату, то:
S12 = (Sкруга – Sквадрата)/4 (2), где Sкруга = p R 2 (3) , а Sквадрата = a 2 (4).
Из рисунка видно, что 4 R 2 = 2 a 2, следовательно a 2 = 2 R 2 и Sквадата = 2 R 2.
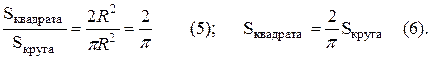 Из (2) – (6) получим:
Из (2) – (6) получим:
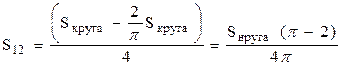 (7), но поскольку полное изменение энтропии за цикл равно D S 0 , то Sкруга = D S 0 = 1 Дж/к, следовательно
(7), но поскольку полное изменение энтропии за цикл равно D S 0 , то Sкруга = D S 0 = 1 Дж/к, следовательно
S12 = D S 0 (p - 2) / 4p, и изменение энтропии D S 12 на участке 1 – 2 равно:
D S 12 = S12 = D S 0 (p - 2) / 4p = 0,09 Дж / К.
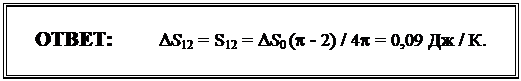
Задача № 66 (6 баллов ) Решение: (ОФ, 2002)
Энтропия конечного состояния не зависит от того, как достигнуто это состояние. Будем считать, что оно достигнуто изобарически, что возможно т. к. конечное давление Pк = P0.
Для каждого сосуда: 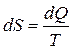
 ,
, 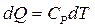 ,
, 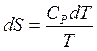 ,
,
а, следовательно, изменения энтропии в обеих бутылях равны:
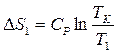 ,
, 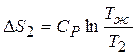 ,где
,где 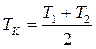 ,
, 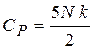 .
.
В итоге полное изменение энтропии равно: 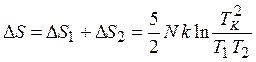
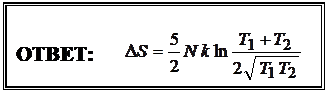
Задача № 67 (6 баллов ) Решение: (РОФ, 2008)

 КПД цикла равен
КПД цикла равен 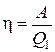 , (1)
, (1)
где работа в цикле равна площади цикла
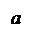
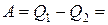
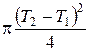 = S круга, (2)
= S круга, (2)
Так как 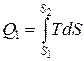 (T dS = dQ),
(T dS = dQ),
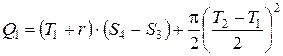 , где
, где 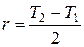 – радиус окружности;
– радиус окружности;
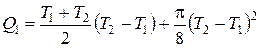 ;
; 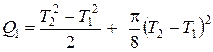 . (3)
. (3)
Подставляем (2) и (3) в (1), преобразовываем:
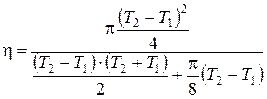 ;
;  ;
;
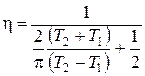 .
.
Если а – сторона квадрата, d – диаметр окружности, то: (Т 2- Т 1) = d; (T 1+ d /2)= a /2; (T 2- d /2)= a /2, т.е. (Т 2+ Т 1)= а, следовательно 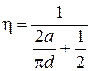 .
.
По условию 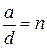 ,
, 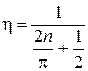

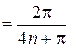
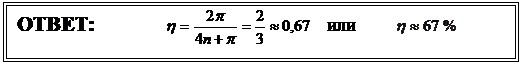 |
Задача № 68 (6 баллов ) Решение: (ОФ, 2003)
Докажем, что треугольник, представленный на графике- прямоугольный.
Если это так, то должны выполняться следующие соотношения:
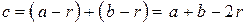 (1) и
(1) и 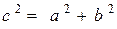 (2).
(2).
Отсюда определим r - радиус окружности, вписанной в прямоугольный треугольник: 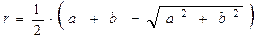 = 1 см (3)
= 1 см (3)
(интересно, кстати, отметить, что справедлива следующая формула для диаметра вписанной в прямоугольный треугольник окружности: 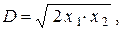 где
где 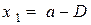 и
и 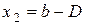 ).
).
Действительно, по условию r = 1 см, следовательно, так как вписанная окружность единственна. рассматриваемый в задаче треугольник- прямоугольный. К такому же выводу придём, выражая угол φ напротив стороны с в произвольном треугольнике, через его полупериметр:
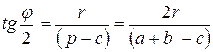 ,
, 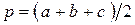 . При φ = 90 0
. При φ = 90 0 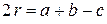 . Отсюда
. Отсюда 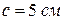 , следовательно,
, следовательно, 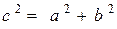 , из чего следует, что треугольник прямоугольный. Тогда становится понятно почему обрадовался инженер- зная радиус окружности., вписанной в такой треугольник, легко рассчитать площадь треугольника S ∆ = p . r = 6, которая в свою очередь определяет искомое изменение энтропии за цикл.
, из чего следует, что треугольник прямоугольный. Тогда становится понятно почему обрадовался инженер- зная радиус окружности., вписанной в такой треугольник, легко рассчитать площадь треугольника S ∆ = p . r = 6, которая в свою очередь определяет искомое изменение энтропии за цикл.
Докажем последнее утверждение. Исходя из выражения для изменения энтропии и определения теплоёмкости, запишем уравнение, связывающее эти две характеристики:
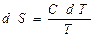 (1), так как по определению-
(1), так как по определению- 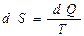 , а
, а 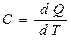 .
.
С учётом того, что C0 и T0 постоянные величины, и представляя dS через
логарифм 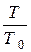 :
: 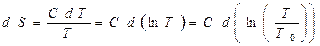 , перепишем (1) в виде:
, перепишем (1) в виде:
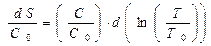 . Следовательно, изменение энтропии за цикл равно:
. Следовательно, изменение энтропии за цикл равно: 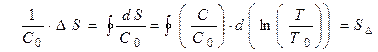 (2). Отсюда окончательно найдём:
(2). Отсюда окончательно найдём:
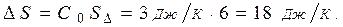
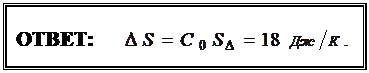
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!