Электростатика. Ответ: Всё просто – прованское масло бурлит не потому, что

ЭЛЕКТРИЧЕСТВО

ФАЗОВЫЕ ПЕРЕХОДЫ

Задача № 71 (1 балл ) Решение: (РОФ, 2007)

ОТВЕТ: Всё просто – прованское масло бурлит не потому, что

достигло температуры кипения, а потому, что испаряется

влага, попавшая из пищи в масло. То есть, другими словами-

кипит не масло, а вода.

Глава III

Задача № 72 ( 2 балла ) Решение: (РОФ, 2005)

Так как уравнение, связывающее потенциал некоторого электростатического поля и его напряжённость имеет вид: 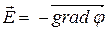(1), то электрическое поле направлено всегда в сторону быстрейшего убывания потенциала. Тогда, начиная с точки 1, потенциал только убывает.

Задача № 73 (7 баллов ) Решение: (РОФ, 2009)

Так как тока в цепи нет – сопротивления из схемы можно исключить.

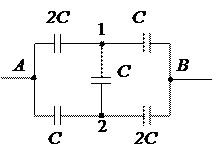
Так как j× С = Q, а узлы 1 и 2 нейтральны, получим:

(j₁-j _A) C ₁ + (j₁ - j₂) C ₅ + (j₁-j _B) C ₃ = 0 (1)

(j₂-j _A) C ₂ + (j₂ - j₁) C ₅ + (j₂-j _B) C ₄ = 0 (2)

или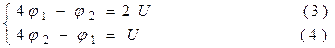

(j _А = U и j _В = 0, т.к. заряд конденсатора определяется только разностью потенциалов). Из (3) и (4) получим:

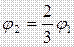(5).

Тогда , (6) и (7)

Искомая электроемкость равна:

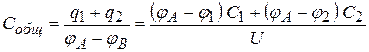, (8)

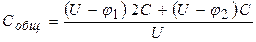. (9)

Подставляя равенства (6) и (7) в (9), найдем:

,

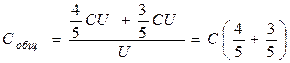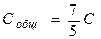
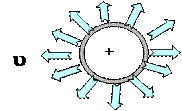Задача № 74 (6 баллов ) Решение: (РОФ, 2004)

Ёмкость сферического проводника совпадает с ёмкостью проводящего шара (так как заряд располагается по поверхности шара, а напряжённость электрического поля внутри него равна нулю) и равна:

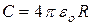(1), а энергия, запасённая в нём в виде электрического поля, равна соответственно:

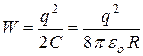(2).

Из закона сохранения энергии следует, что модули изменения кинетической и потенциальной энергий любой замкнутой системы одинаковы на любом произвольно выбранном отрезке времени. Тогда выполняется равенство:

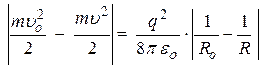(3).

Отсюда скорость разлёта осколков на расстоянии R от места взрыва равна:

(4).

Наибольшее значение скорости достигается на бесконечности, то есть при ∞: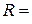

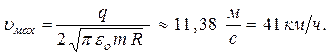
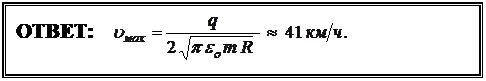
Задача № 75 ( 8 баллов ) Решение: (РОФ, 2006)

Сила, действующая на элемент

кольца с зарядом dq, равна:

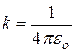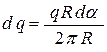, где . Из рисунка получим: , причём заряд равен (1). или 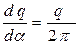(2).

Таким образом (учитывая, что sin dα ≈ dα) получим:

(2).

Окончательно найдём искомую силу растяжения, возникающую в заряженном кольце:

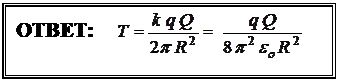
Задача № 76 ( 9 баллов ) Решение: (ОФ, 2005)

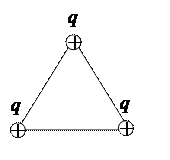
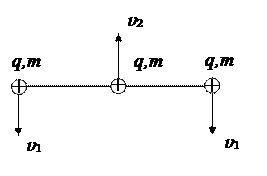
Скорости зарядов будут максимальны в тот момент времени, когда они будут находится на одной прямой.

Из закона сохранения импульса:

2 mv ₁ = mv ₂.

Изменение потенциальной энергии W ₁- W ₂ системы зарядов равно их общей кинетической энергии- Е_кин

,

.

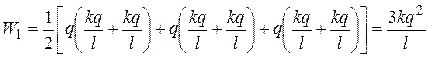
и ,

,

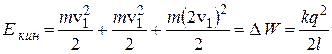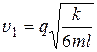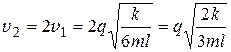
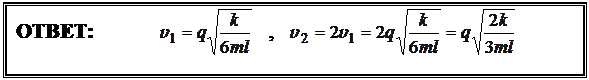
Задача № 77 ( 7 баллов ) Решение: (РОФ, 2008)

Так как j× С = Q, а узлы 1 и 2 нейтральны, получим:

(j₁-j _A) C ₁ + (j₁ - j₂) C ₅ + (j₁-j _B) C ₃ = 0 (1)

(j₂-j _A) C ₂ + (j₂ - j₁) C ₅ + (j₂-j _B) C ₄ = 0 (2)

или

(j _А = U и j _В = 0, т.к. заряд конденсатора определяется только разностью потенциалов)

Из (3) и (4) получим: 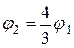(5), а 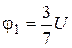(6)

Отсюда найдём: 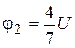. (7)

Искомая электроемкость равна:

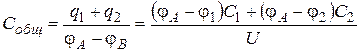, (8)

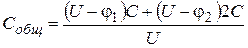. (9)

Подставляя равенства (6) и (7) в (9), найдем:

,

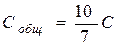
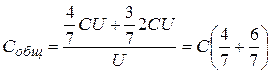Задача № 78 ( 6 баллов ) Решение: (ОФ, 2009)

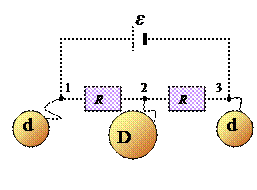
Пусть Q ₁ , Q ₂ и Q ₃ -заряды шаров после их подсоединения к цепи. Так как шары первоначально не заряжены, то:

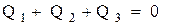(1)

(заряд на электрической цепи и соединительных проводниках мал).Общий заряд цепи не меняется и равен нулю: Q _общ = 0 (2).

Найдём разность потенциалов между точками 1-2 и 2-3:

и

или Из уравнений (4) и (1) следует равенство: (5). Тогда из (3) и (5) получим:

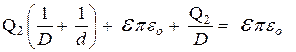или Q ₂ = 0 (6). Тогда из (3) и (1):

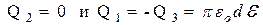
Задача № 79 ( 8 баллов ) Решение: (РОФ, 2005)

1) Вслед за рассуждениями инженера получим схему:

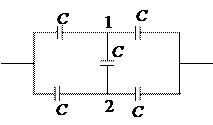Так как потенциалы точек 1 и 2 равны из соображений симметрии- средний конденсатор не будет заряжен и его можно удалить из схемы не изменяя при этом её общую ёмкость.

В результате таких рассуждений имеем эквивалентную схему:

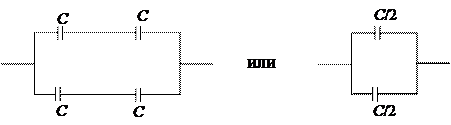В итоге получаем: C ₁ = C. (1)

2) На самом деле исключать из схемы участки с сопротивлениями R нельзя. Точнее говоря, исключить-то их можно (ведь тока в них нет), но нельзя при этом выбросить из схемы и те участки, на которых они находились!

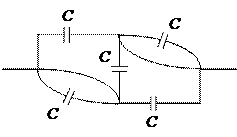При любом значении сопротивления R ток в них отсутствует и, следовательно, можно рассмотреть частный случай, когда R = 0. Тогда схему можно нарисовать так:

Таким образом, становится очевидным, что нижний левый и верхний правый конденсаторы при их подключении к источнику тока не будут заряжаться, а следовательно их можно исключить из схемы не изменяя при этом общей ёмкости схемы.

В результате получаем C ₂ = 3 C. (2) Сравнивая (1) и (2), получим: С₂/С₁ = 3

Дата добавления: 2014-12-08