
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теплоёмкость. Определим, как с течением времени меняется толщина льда
|
|
|
|
Задача № 60 ( 5 баллов ) Решение: (РОФ, 2008)
Определим, как с течением времени меняется толщина льда.
По закону Фурье 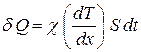 (1),
(1),
где d Q – количество теплоты, отнятое у слоя воды подо льдом.
Если при этом весь слой воды превратится в лед, то отведенная теплота будет равна: 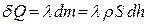 . (2)
. (2)
Из (2) и (3): 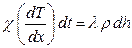 . (3)
. (3)
Так как градиент температуры величина постоянная при данной фиксированной толщине льда, то: 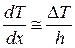 , подставляем последнее равенство в (3):
, подставляем последнее равенство в (3): 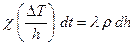 . (4). Из (4) получим:
. (4). Из (4) получим: 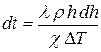 (5).
(5).
Интегрируем последнее выражение:  или
или 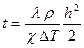 (6).
(6).
Таким образом, так как 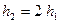 и
и  , то верно:
, то верно: 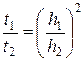 .
.
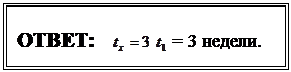 |
Получим:
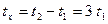 = 3 недели.
= 3 недели.
Задача № 61 (7 баллов ) Решение: (РОФ, 2006)
В результате двух переливаний масса воды в обоих сосудах не изменилась. По условию температура чая со смородиной уменьшилась на ΔТ1 = 10 0С
и стала равной Т1′ = 75 0С, а температура воды во втором термосе увеличилась с Т2 = 25 0С до Т2′. Определим Т2 ′ с учётом того, что после двух переливаний убыль тепловой энергии воды первого термоса равна прибыли тепловой энергии во втором термосе. Запишем:
ΔQ1= c m1ΔТ1 = ΔQ2= c m2 ΔТ2 или m1ΔТ1 = m2 ΔТ2 (1).
Отсюда получим:
m1 ΔТ1= m2 (Т2′- Т2) или Т2′ = m1 ΔТ1/ m2 + Т2 = 40 0С (2).

Этого значения достигает температура порции горячего чая Δm из первого термоса после первого переливания. Убыль энергии при этом: Δq 1 = cΔ m (Т1-Т2′) (3) равна приросту энергии холодного чая Δq 2 = c m2 (Т2′- Т2) или 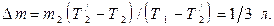
Задача № 62 (3 балла ) Решение: (РТ ОФШ 11кл, 2006)
Для определения удельной теплоемкости смеси используем закон сохранения энергии. Количество теплоты Q, необходимое для нагревания смеси, расходуется на нагревание песка Q1 и цемента Q2
Q = Q1+Q2 (1),
где Q = Cсм(m+2m)ΔT – количество теплоты для смеси
Q1 = Cпеска·mΔT – количество теплоты для песка (2),
Q2 = Cцем·2mΔT – количество теплоты для цемента (3).
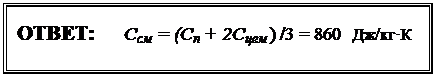 |
Из уравнений (1) – (3) найдём значение для теплоемкости смеси.
Задача № 63 (7 баллов ) Решение: (РОФ, 2001)
Зависимость теплоемкости от температуры можно представить в виде:
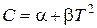 . (1)
. (1)
Выразим коэффициент b через Т 0. В состоянии А 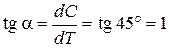 , т.е.
, т.е. 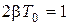 , откуда
, откуда  . Зависимость (1) принимает вид:
. Зависимость (1) принимает вид:
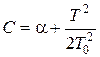 . (2)
. (2)
Применим первый закон термодинамики
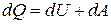 . (3)
. (3)
Выразим количество теплоты из определения теплоемкости 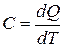 :
:
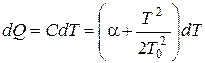 ,
,
изменение внутренней энергии – через хорошо известную теплоемкость при постоянном объеме 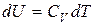 , а также применим выражение для работы при термодинамических процессах
, а также применим выражение для работы при термодинамических процессах 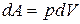 . Подставим полученные выражения в (3):
. Подставим полученные выражения в (3):
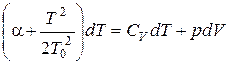 .
.
В это уравнение входят три переменные. Для исключения из уравнения давления p воспользуемся уравнением состояния идеального газа, то есть уравнением Менделеева – Клапейрона: 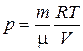 ,
,
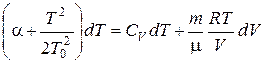 .
.
Разделяя переменные
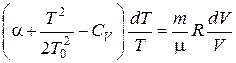 и произведя интегрирование, получаем:
и произведя интегрирование, получаем:
 или
или 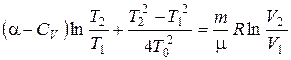 (4).
(4).
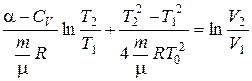 или
или 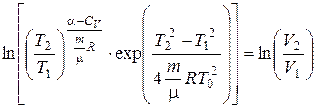 ,
,
Отсюда окончательно находим отношение объёмов V2 /V1 .

|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 454; Нарушение авторских прав?; Мы поможем в написании вашей работы!