Уравнение состояния идеального газа

И ТЕРМОДИНАМИКА

МОЛЕКУЛЯРНАЯ ФИЗИКА

Задача № 47 (4 балла ) Решение: (ОФ, 2003)

Плотность газа, составляющего шаровую молнию, равна плотности воздуха,

так как молния свободно плавает в воздухе, то: r = r₀,

равны, очевидно, и давления: Р = Р ₀.

Уравнение Менделеева – Клапейрона:

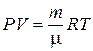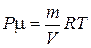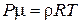, , или .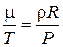

Правые части последнего уравнения равны для воздуха и газа, составляющего молнию, следовательно, равны и левые части:

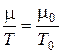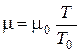; = 86 г/моль (m₀ = 29 г/моль).

Искомое число молекул воды, связанных с ионом азота, найдем из соотношения: .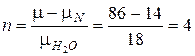

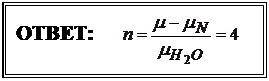
Задача № 48 (5 баллов ) Решение: (ОФ, 2005)

В соответствии с I- м началом термодинамики, при изохорном процессе

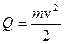(1). С другой стороны (2). Приравняв (1) и (2), получим: 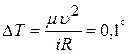С.

Такой же ответ можно получить, рассуждая по- другому:

На каждую степень свободы молекулы приходится в среднем энергия 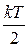, а после удара к этой энергии добавится 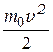. Тогда: 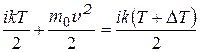. Из полученного равенства найдём :

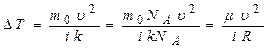= 0,1°С.

Задача № 49 ( 8 баллов ) Решение: (РОФ, 2005)

При изотермическом процессе изменение энтропии 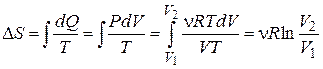. Поскольку при каждом изотермическом расширении объем газа увеличивается в одно и то же число раз, 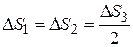. (1)

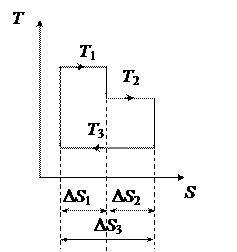
Нарисуем данный цикл в координатах T, S.

К.П.Д. теплового цикла

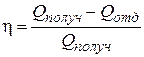. (2)

Газ получает тепло при изотермических расширениях , (3)

и отдает тепло при изотермическом сжатии

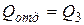. (4)

(3) и (4) подставим в (2)

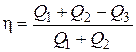. (5)

При изотермическом процессе 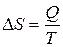, тогда:

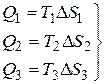с учетом (1) 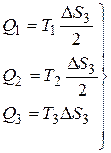подставляя в (5), получим:

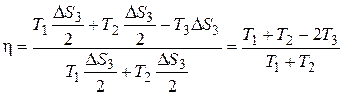. Окончательно найдём:

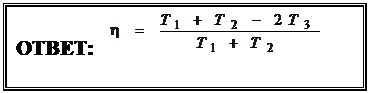Задача № 50 ( 4 балла ) Решение: (ОФ, 2003)

Пусть индексы 1 и 2 обозначают соответственно- атомарный (I) и молекулярный йод (I ₂ ). По условию задачи имеем:

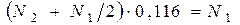(1),

где 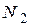- число молекул, а 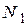- число атомов йода в сосуде.

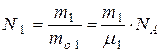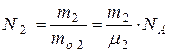Так как: (2) и (3),

где 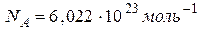- число Авогадро, то:

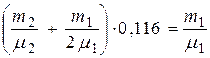или 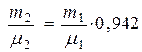(4). Перепишем (4)

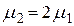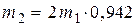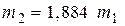с учётом того, что молярная масса молекулярного йода в 2 раза больше, чем у атомарного () в виде: или (5).

Молярная масса атомарного йода равна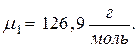

С другой стороны, по закону Дальтона- давление смеси газов равно сумме, так называемых, парциальных давлений. Парциальное давление – давление газа в данном сосуде, создаваемое им в отсутствии других газов.

Тогда получим:

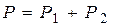(6), где 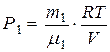(7) и 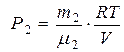(8). Из (6) – (8) найдём: 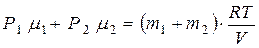(9) и

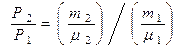или с учётом (4) получим: 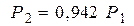(10).

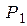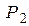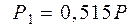Решив линейную систему из двух уравнений (6) и (10), определим и :

и .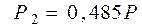

Искомую массу паров йода в сосуде 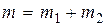определим из уравнения (9):

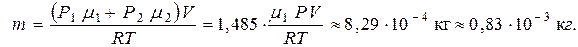
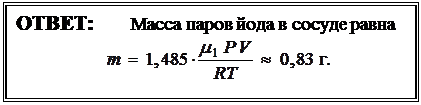Задача № 51 (3 баллов ) Решение: (РОФ, 2000)

Так как по условию все три процесса очень быстрые, то все они являются адиабатическими.

Учитывая, что показатель адиабаты не изменяется (поскольку не меняется состав газа), придём к выводу, что все три точки на PV -диаграмме состояния идеального газа принадлежат одной адиабате.

Искомая работа газа в замкнутом процессе 1-2-3-1 равна площади цикла на PV – диаграмме, которая в данном случае равна нулю.

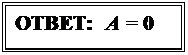
Задача № 52 (4 балла ) Решение: (ОФ, 2006)

Определим величину разности работ A₁₃ и A₁₂. Разность ΔA = A₁₃ - A₁₂ равна ΔS:

ΔS = ½ ((P₂ – P₃)V₁ + P₁ (V₃ – V₂))

где S - площадь под соответствующим участком

1-2 или 1-3. Так как ΔS, очевидно,положительная

величина ((P₂ – P₃)V₁ + P₁ (V₃ – V₂)) > 0, то по первому началу термодинамики получим:

ΔQ ₁₂ = A₁₂ + ΔU₁₂ и ΔQ ₁₃= A₁₃ + ΔU₁₃.С учётом того, что ΔU₁₂ = ΔU₁₃, а также учитывая, что ΔA₁₂ < ΔA₁₃ , получим: Δ Q ₁₃ > Δ Q ₁₂.

ОТВЕТ: Δ Q ₁₃ > Δ Q ₁₂

Задача № 53 ( 6 баллов ) Решение: (РОФ, 1999)

Определим сначала ускорение свободного падения на поверхности данной планеты.

Запишем для тела массы m: 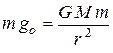(1). Отсюда: 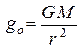(2).

Давление, создаваемое атмосферным столбом h, равно: 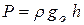(3), при этом 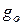считаем независящим от высоты, т.к. h «r.

Из уравнения Менделеева - Клапейрона (PV = 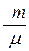RT) получим: 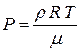(4). Тогда из уравнений (2), (3) и (4) получим: 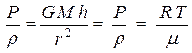или 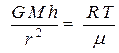. Окончательно получим:

Задача № 54 (3 балла ) Решение: (РТ ОФШ 10 кл, 2006)

Полагая приближённо, что при всплытии воздушного пузыря температура воздуха внутри него практически постоянна, запишем в соответствии с законом Бойля-Мариотта для идеального газа: PV = Const или P₁ V₁ = P ₂ V₂.

Рассматривая соответствующие давления и объёмы на дне и на поверхности, получим следующее уравнение для определения h:

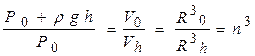или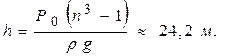

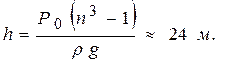
Задача № 55 (5 баллов ) Решение: (РОФ, 2007)

Двигатели НЛО совершают работу над газом, увеличивая его кинетическую энергию. Считая, что в расчёте на единицу времени из двигателей выбрасывается масса газа, равная µ и все частицы газа имеют одинаковые скорости υ, мощность двигателей «тарелки» в момент её зависания равна: 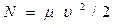(1).

Учитывая, что сила тяги двигателей (реактивная сила) равна F = - µ υ, и условие зависания «объекта» (считая, как обычно, лабораторную систему отсчёта инерциальной) имеет вид M g + F = 0, получим:

N = M g υ /2 (2). Отсюда определим ускорение свободного падения:

g = 2N / M υ. (3).

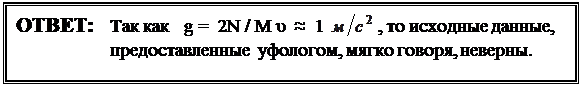
Задача № 56 (4 балла ) Решение: (РОФ, 2007)

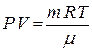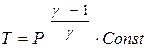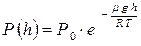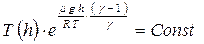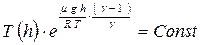Поскольку движение воздуха вверх совершается достаточно быстро возможно рассматривать процесс расширения газа адиабатическим. Тогда из уравнения Пуассона , а также из уравнения Менделеева – Клапейрона: найдём . С учётом барометрической формулы получим зависимость температуры от высоты: или или 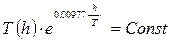. Для h менее ≈ 3 км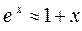

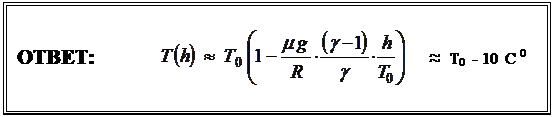Отсюда окончательно получим:

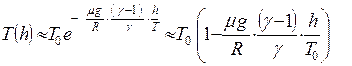
Задача № 57 (4 балла ) Решение: (РОФ, 2010)

Во-первых,давление и концентрация n идеального газа прямо пропорциональны друг другу 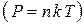, а во-вторых, исходя из определения идеальности газа, один идеальный газ не влияет на поведение другого 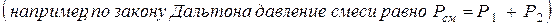. Таким образом, концентрация газов с разными молярными массами по-разному убывает с высотой. При этом её значение определяется барометрической формулой- частным случаем распределения Больцмана: 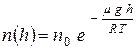(1).

Применяя данную формулу для азота и кислорода, найдём:

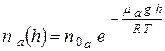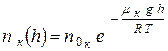(2) и (3).

Поделив равенства (2) и (3), запишем: 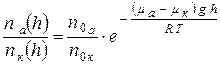(4).

По условию 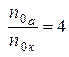, тогда получим: 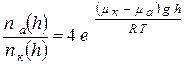(5).

Искомая доля кислорода (молярная) в воздухе в районе Цинхай определяется выражением:

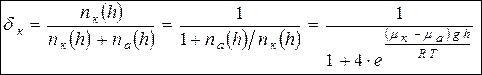(6).

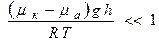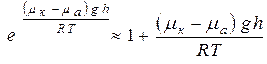Так как , то: (7).

С учётом (7) получим искомую величину из выражения (6):

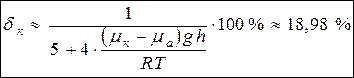(8).

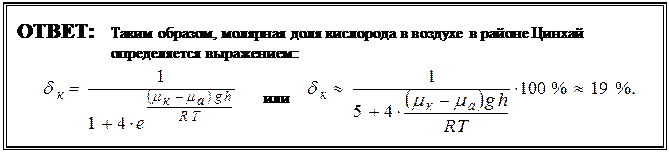P.S. Интересно отметить, что при восхождении на высоты от 3500 м выше, возникает горная болезнь- насыщение крови кислородом составляет менее 90 %. Начиная с высоты 5800 м, идёт “зона смерти”. Так, например, при восхождении на Эверест (по-тибетски- Джомолунгма “Божественная мать Земли”) самую высокую (8848 м) гору из 14 –ти “восьмитысячников” нашей планеты, альпинисты обязательно берут с собой титановый баллончик с кислородом, поскольку на вершине Эвереста плотность воздуха уменьшается почти в три раза.

Задача № 58 (6 баллов ) Решение: (РОФ, 2009)

А) Если 0 < 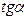< 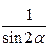., то 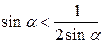. Тогда 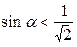. Следовательно, угол α не больше 45 ⁰ , а значит 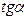< 1. По условию 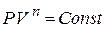или 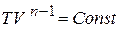. Таким образом, температура с увеличением объёма растёт по закону 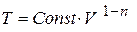, где n < 1.

B) Выяснив, что 0 < n < 1, можно прийти к ответу, рассуждая следующим образом:

Кривые процесса 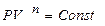идут, при указанных значениях n на графике зависимости P от V, более полого, чем проведённые через первоначальную точку изотермы 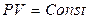. Следовательно, при расширении газа по этому закону давление падает медленнее, чем при изотермическом процессе расширения газа. Таким образом – газ нагревается!

Задача № 59 (5 баллов ) Решение: (РОФ, 2004)

Температура оболочки падающего метеорита равна в первом приближении температуре “воздушной подушки” перед метеоритом. Нагрев воздуха вызван в основном его быстрым сжатием.

Так как процесс сжатия очень быстрый, то его можно считать адиабатическим. Из уравнения Пуассона следует, что

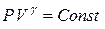(1), где показатель адиабаты 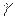связан с числом степеней свободы газа i (для воздуха, состоящего в основном из двухатомных газов- азота (78 %) и кислорода (21 %) i = 5) следующим выражением: 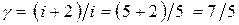(2).

Пренебрегая краевыми эффектами (воздух частично успевает огибать края огромного метеорита), запишем в соответствии с законом Менделеева - Клапейрона: 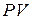~ 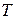(3). Таким образом, исключая 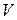из (1)–(3), получим: 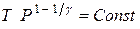(4) или (5).

Отсюда окончательно найдём температуру 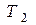на поверхности падающего метеорита:

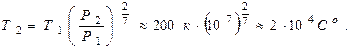
Дата добавления: 2014-12-08