Пример выполнения задачи 8

Задача 8 относится к плоскому движению твердого тела. Скорость ползуна для данного положения механизма можно вычислить как при помощи теоремы о проекции скоростей двух точек тела, так и с помощью мгновенного центра скоростей шатуна.

Для этого необходимо знать скорость какой-нибудь точки шатуна (например, точки А) и направление скорости ползуна.

Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярные направления. В качестве полюса удобно принять точку А.

Решение задачи 8 рассмотрим на примере варианта, соответствующего шифру 000. Из таблицы 8 принимаем схему Х, (рис. 8.1).

Рис. 8.1.

1. Скорость точки А, как вращательную вокруг неподвижной точки О, определим по равенству

. u

Для определения скорости точки В определим положение мгновенного центра скоростей Р, для чего покажем направления скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям и . Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р.

Рассматривая плоское движение шатуна в данный момент времени как вращательное относительно мгновенного центра скоростей Р, определим угловую скоростей шатуна

=

Расстояние АР определим из АВР по теореме синусов

= =

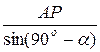АР = АВ =80 см

= =0,8 рад/с.

Скорость точки В определим как вращательную относительно мгновенного центра скоростей Р

= ВР;

из АВР: ВР = =

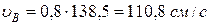
2. Ускорение ползуна В определим с помощью векторного равенства

= + + , (*)

Здесь – ускорение точки А, выбранной за полюс;

– осестремительное ускорение;

– вращательное ускорение точки В во вращательном движении вокруг полюса.

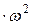Ускорение точки А кривошипа при равномерном его вращении вокруг неподвижной оси О состоит только из осестремительной составляющей = . Модуль ускорения точки А определяется равенством = =ОА =64 =64 см/с².

Осестремительное ускорение точки В относительно точки А определяется по формуле

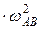=АВ =80 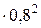=51,2 см/с²

Проектируя векторное равенство (*) на ось u, проходящую через точки А и В, получим

= - +

отсюда

см/с².

Из векторного равенства видно, что вектор ускорения точки В направлен в ту же сторону, что и вектор скорости (рис.8.1).

Задача 9. Решение второй задачи динамики материальной точки

Условие №1. Тяжелая материальная точка М брошена под углом к горизонту со скоростью . В начальный момент времени точка находилась в положении 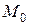. Пренебрегая сопротивлением среды, определить уравнения движения точки.

Условие №2. Тело М весом 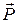брошено вертикально вверх (схема V) или вниз (схема VI) со скоростью . При движении на тело действует сила ветра 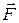. В начальный момент времени тело находилось в положении 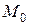. Определить уравнения движения тела.

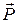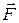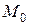Условие №3. Груз весом движется прямолинейно по горизонтальной плоскости. На груз действует сила , составляющая с горизонталью угол . Коэффициент трения скольжения груза о плоскость равен f. В начальный момент времени (положение ) груз находился на расстоянии а от начала координат и имел скорость . Определить уравнение движения груза.

Условие №4. Груз весом 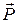движется вверх (схема IX) или вниз (схема X) по негладкой наклонной плоскости. Коэффициент трения скольжения груза о плоскость равен f. В начальный момент времени (положение 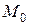) груз находился на расстоянии а от начала координат и имел скорость . Определить уравнение движения груза.

Примечание. Для схем VIII и IX определить уравнение движения груза на первом этапе, когда движение происходит в направлении начальной скорости.

Схемы к задаче приведены на рис. 9, численные данные – в табл. 9.

Таблица 9

Цифры шифра	2-я цифра шифра	3-я цифра шифра	1-я цифра шифра	3-я цифра шифра
,	номер условия	номер схемы	f	, град	а, м	b, м	F, Н	P, Н
			I	-		4,5	2,0	-	-
			II	-		5,0	2,5	-	-
			III	-		5,5	3,0	-	-
			IV	-		6,5	3,5	-	-
			V	-		6,5	-
			VI	-		7,0	-
			VII	0,10		7,5	-
			VIII	0,12		8,0	-
			IX	0,14		8,5	-	-
			X	0,16		9,0	-	-

Рис. 9
Пример выполнения задачи 9

При решении задачи 9 следует изобразить движущееся тело в произвольном положении и показать все действующие на тело силы. Затем составить дифференциальные уравнения движения (два при криволинейном и одно при прямолинейном движениях) и проинтегрировать их. Значения постоянных интегрирования определить из начальных условий.

В качестве примера рассмотрим решение задачи 9(условие №4), соответствующей варианту по шифру 000. По данным таблицы 9 принимаем схему Х, =30м/с, =0,16, , а=9м (рис. 9.1).

Рис. 9.1.

1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (наклонной плоскости) и приложим к телу реакцию связи в виде нормальной составляющей и силы трения . Тогда наряду с активной силой 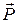(весом тела) на тело будет действовать система трех сил (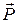, , ), под действием которых тело будет совершать движение по шероховатой наклонной плоскости.

2. Примем тело за материальную точку. Проектируя основное уравнение динамики точки на оси декартовых координат Ох и Оy (ось Ох совпадает с направлением движения точки), получим два дифференциальных уравнения

- , (1)

. (2)

Здесь m – масса точки; – проекции ускорения точки на соответствующие оси. Так как тело движется прямолинейно вдоль оси Ох, то проекция ускорения на ось Оy равна нулю. Следовательно, имеем =0 (3)

Сила трения по закону Кулона равна = (4)

Уравнения (1-4) образуют замкнутую систему, из которой определим уравнение движения тела по шероховатой наклонной плоскости.

Из уравнения (4) с учетом уравнений (2) и (3) получим

=

Подставляя в уравнение (1), получим дифференциальное уравнение

После замены 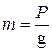и , где – ускорение свободного падения тела, а – скорость тела, получим

= .

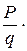
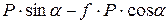Разделив переменные и сделав очевидные преобразования, проинтегрируем дифференциальное уравнение с учетом начальных условий (при )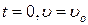

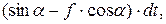
(5)

Проинтегрируем еще раз равенство (5) с учетом и начальных условий (при ).

(6)

Подставив в полученное равенство значения заданных величин, окончательно получим уравнение движения груза

Задача 10. Применение теоремы об изменении кинетической энергии для определения скорости тела

Однородный каток В весом 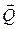и радиусом R соединен гибкой нерастяжимой нитью с грузом А весом 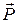. Нить переброшена через невесомый блок О радиуса r. К оси катка С (схемы I-V) или к грузу А (схемы VI-VIII) или к свободному концу нити (схемы IX-X) приложена сила , зависящая от величины перемещения s. Каток катится без скольжения; коэффициент трения скольжения груза о плоскость равен f, момент сил сопротивления в подшипнике блока равен М. Определить скорость груза А, когда он переместится на величину s. В начальный момент времени система находилась в покое.

Схемы к задаче приведены на рис. 10, численные данные – в табл. 10.

Таблица 10

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра
номер схемы	, град	f	r, см	s, м	M, Нм	силы, кН
P	Q	F
	I		0,06		2,1		1,1	3,1
	II		0,07		2,2		1,2	3,3
	III		0,08		2,3		1,3	3,3
	IV		0,09		2,4		1,4	3,4
	V		0,10		2,5		1,5	3,5
	VI		0,06		2,6		1,6	3,6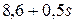
	VII		0,07		2,7		1,7	3,7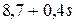
	VIII		0,08		2,8		1,8	3,8
	IX		0,09		2,9		1,9	3,9
	X		0,10		3,0		2,0	4,0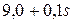

Рис. 10
Пример выполнения задачи 10

Задачу 10 надо решить, применив теорему об изменении кинетической энергии системы (каток-груз-нить-блок). Для этого необходимо: на рисунке изобразить все силы и вычислить их работу на заданном перемещении; вычислить кинетическую энергию системы в начальном и конечном положениях.

Решим задачу 10 по варианту, соответствующему условному шифру 000. По данным таблицы 10 принимаем схему Х, , (рис. 10.1).

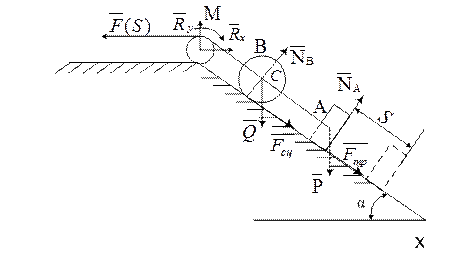
Рис. 10.1.

Система сил, действующих в данной системе: активные силы (), реакции связей () и момент трения в блоке .

По теореме об изменении кинетической энергии системы:

(1)

Здесь и – кинетическая энергия системы соответственно в данный и начальный момент времен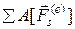и; и – суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.

По условию задачи, система в начальный момент находилась в покое, следовательно, =0 (2). Кроме того, тела системы абсолютно твердые, а нить гибкая и нерастяжимая, то

(3)

Кинетическая энергия системы (каток-груз) в данный момент времени равна

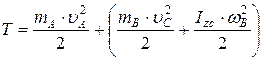(4)

Здесь и – массы груза и катка;

– момент инерции катка относительно оси вращения;

– скорость груза и точки катка; – угловая скорость катка. Подставляя эти величины в равенство (4) получим:

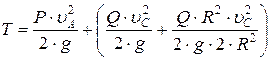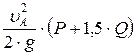= . (5)

Сумма работ всех внешних сил системы равна

= /

Работа сил и равна нулю, так как направления этих сил составляют прямой угол с направлением скоростей и . Работа силы сцепления и сил реакции и равны 0, так как эти силы приложены к неподвижной точке. Работу сил определим следующим образом:

= = =

=

=

=

= =

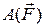Таким образом

= (6)

Подставляя равенства (2), (3), (5), (6) в выражении (1), окончательно получим:

=

Отсюда скорость груза А, когда он переместится на величину =3м, будет равна

= =

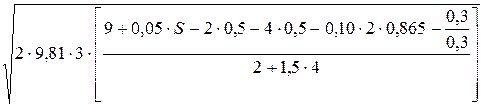=6,05 .

Задача 11. Применение принципа Даламбера для определения реакций опор

К вертикальному валу весом 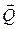жестко приварен невесомый стержень длиной l₁, с точечным грузом М весом на конце и тонкий однородный стержень CD длиной l₂ и весом , лежащие в одной плоскости. Определить реакции подпятника А и цилиндрического подшипника В, если вал вращается равномерно со скоростью n оборотов в минуту.

Схемы к задаче приведены на рис. 11, численные данные – в табл. 11.

Таблица 11

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра
номер схемы	, град	n,	силы, Н	длины, см
Q	P1	P2	a	b	l1	l2
	I
	II
	III
	IV
	V
	VI
	VII
	VIII
	IX
	X

Рис. 11

Дата добавления: 2014-12-08