Пример выполнения задачи 2

Задача 2 относится к равновесию тела (балки) под действием плоской системы сил. Для определения реакций опор необходимо составить три уравнения равновесия для балки, приложив к ней активные (заданные) силы и силы реакций связей (опорные реакции).

При вычислении момента силы 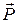относительно выбранной точки иногда бывает удобно разложить эту силу на две составляющие и найти момент силы 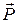как сумму моментов этих составляющих.

Распределенная нагрузка, приходящаяся на единицу длины, называется интенсивностью нагрузки и обозначается обычно буквой q. Равнодействующая распределенной нагрузки равна грузовой площади (площади эпюры нагрузки) и приложена в центре тяжести этой площади.

Рассмотрим вариант решения задачи 2, соответствующей условному шифру 000. Схема балки с указанием численных значений заданных величин из таблицы 2 приведена на рисунке 2.1.

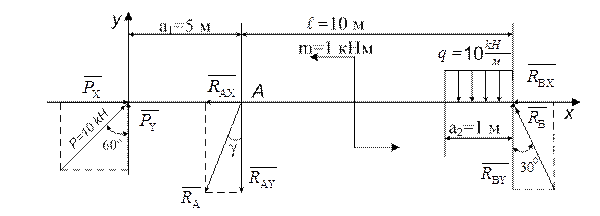Рис. 2.1.

Для решения этой задачи условия равновесия удобнее принять в следующей форме:

1)

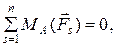
2)

3)

Записывая эти условия для данной задачи, получим три уравнения, которые содержат по одной неизвестной. Решаем их.

1) 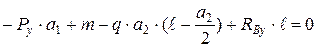, где

кН

Так как направление реакции стержня ВС известно, то

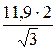= =13,7кН,

= = =6,87кН

2)

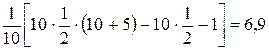кН.

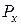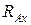3) - - =0, где = ,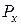

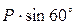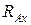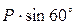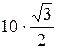= - = - = =1,79кН

Сила реакции связи в точке А равна

= =7,13кН

и направлена под углом 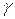к вертикали

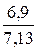= =0,968, 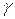=14,5^о .
Задача 3. Равновесие вала под действием пространственной системы сил

Условие №1. На горизонтальный вал, который может вращаться в подшипниках A и B, насажены два шкива. Радиусы шкивов равны 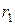=12 см, 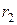=16 см; ветви ремней каждого шкива параллельны между собой и образуют соответственно углы 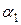с горизонталью и с вертикалью. Пренебрегая весами шкивов и вала, найти натяжения ведущей и ведомой ветви ремня, а также реакции подшипников при равновесии вала.

Примечание. Натяжение ведущей ветви ремня принять вдвое больше натяжения ведомой (, ).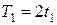

Условие №2. На горизонтальный вал насажены два колеса с радиусами 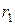=12 см, 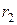=16 см и прикреплён перпендикулярно оси вала горизонтальный рычаг CD длиной l =20 см. К одному колесу приложена сила 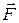, образующая с горизонталью угол 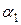, а к другому – сила 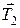, образующая с вертикалью угол ; к рычагу приложена вертикальная сила 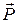. Пренебрегая весами вала, колёс и рычага, определить силу 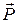, при которой вал находится в равновесии, а также реакции подшипников A и B.

Условие №3. На горизонтальный вал насажено колесо радиуса 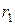=12 см и прикреплён перпендикулярно оси вала рычаг CD длиной l =20 см, образующий с горизонтальной плоскостью угол . Верёвка, намотанная на колесо и натягиваемая грузом 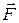, сходит с него по касательной, наклонённой под углом 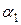к горизонту. Пренебрегая весами вала, колеса и рычага и трением в блоке, определить вертикальную силу 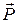, при которой вал находится в равновесии, а также реакции подшипников A и B.

Схемы к задаче приведены на рис. 3, численные данные – в табл. 3.

Таблица 3

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра	1-я цифра шифра
номер условия	номер схемы	Расстояния, м	Углы, град	Силы, Н
a	b	c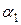
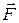
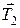
		I	1,0	1,0	1,0
		II	1,2	1,2	1,2
		III	1,4	1,4	1,4
		IV	1,6	1,6	1,6
		V	1,5	1,5	1,5
		VI	1,0	1,0	1,0
		VII	1,2	1,2	1,2
		VIII	1,4	1,4	1,4
		IX	1,6	1,6	1,6
		X	1,8	1,8	1,8

Рис. 3
Пример выполнения задачи 3

В задаче 3 рассматривается равновесие тела (вала) под действием системы сил, произвольно расположенных в пространстве. При решении этой задачи, так же как и в двух предыдущих, следует заменить наложенные на тело связи их реакциями. Для определения искомых величин надо составить шесть уравнений равновесия.

Следует иметь в виду, что при нахождении проекции силы на ось часто бывает проще сначала найти ее проекцию на координатную плоскость, в которой расположена эта ось, а затем найденную проекцию спроектировать на данную ось. Точно так же при определении момента силы относительно оси нередко бывает удобно разложить силу на взаимно перпендикулярные составляющие, одна из которых параллельна какой-нибудь координатной оси.

Решим, для примера, вариант задачи 3, соответствующий условному шифру 000. Схема вала с указанием численных размеров заданных величин из таблицы 3 приведена на рис. 3.1.

Рис. 3.1.

К валу кроме силы 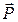, приложенной к рычагу CD, приложена сила натяжения веревки, равная весу груза 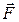, так как по условию задачи, трения в блоке нет. Реакции подшипников и 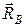, расположенные в плоскостях, перпендикулярных оси y, разложим на взаимно перпендикулярные составляющие соответственно , и , 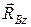. Направление составляющих выбирается произвольно.

Составляя условия равновесия для вала, получим шесть уравнений, из которых одно выполняется тождественно.

1) - +

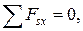
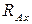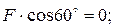
2)

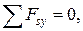
3) - + +

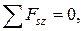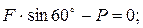
4) +

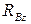
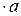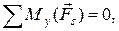
5) 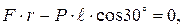где r =0,12м, =СА=0,2м;

6)

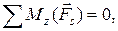
Из (6) = 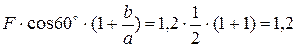кН

Из (5) кН

Из (4) кН

Из (3) кН

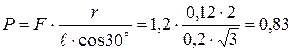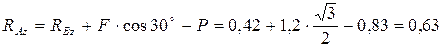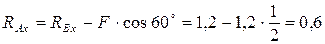Из (1) кН

Силы реакций подшипников и их направление

= кН,

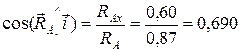(46,4^о);

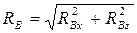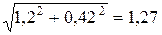= кН,

(19,1^о).

Задача 4. Определение центра тяжести плоской фигуры

Определить положение центра тяжести плоской фигуры.

Схемы к задаче приведены на рис. 4, численные данные – в табл. 4.

Таблица 4

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра
номер схемы	а, см	b, см
	I
	II
	III
	IV
	V
	VI
	VII
	VIII
	IX
	X

Рис. 4
Пример выполнения задачи 4

Для решения задачи 4 следует мысленно разбить плоскую фигуру на такие части, положения центров тяжести которых известны или легко могут быть определены. При этом часто бывает удобно заменить данную фигуру не суммой, а разностью отдельных её частей. Следует помнить, что вычисления можно существенно упростить удачным выбором осей координат.

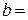В качестве примера решим задачу 4 по варианту, соответствующему условному шифру 000. Для этого шифра из последней строки таблицы 4 принимаем: схема X, =100 см, 100 см.

Рис. 4.1

Представим данную фигуру (рис. 4.1), состоящей из 3-х частей: 1-я часть – прямоугольник (0,5 b x0,2 a), 2-я часть – прямоугольник (0,1 b x0,8 a), третья часть – треугольник. Возьмем систему декартовых координат xOy. Для расчета координат центра тяжести составим таблицу.

Номер части
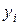
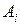
	0,5 b	0,1 a	0,2 ab	0,02 a^2b	0,1 ab^2
	0,35 b	0,6 a	0,08 ab	0,048 a^2b	0,028 ab^2
	0,6 b	0,33 a	0,12 ab	0,04 a^2b	0,072 ab^2
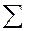
	0,4 ab	0,108 a^2b	0,2 ab^2

см;

см.

Задача 5. Кинематика точки

Движение точки задано уравнениями в декартовых координатах , , 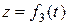(x, y, z в см, t в с). Определить величину и направление скорости и ускорения точки и радиус кривизны траектории в момент времени .

Примечание. При определении скорости, ускорения и радиуса кривизны траектории для упрощения вычислений использовать значения проекций скорости и ускорения для заданного момента времени.

Численные данные приведены в табл. 5.

Таблица 5

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра	2-я цифра шифра
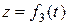, см	, см	, см	, см

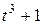
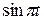
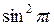
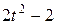
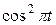
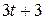
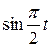
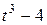
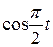
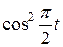
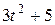
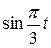
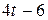
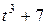
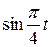
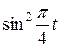
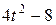
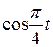
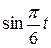
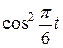
Дата добавления: 2014-12-08