Введение. Курс «Прикладная механика» является основой формирования инженерного мышления слушателей и курсантов Уральского института ГПС МЧС РФ и структурно состоит из

Курс «Прикладная механика» является основой формирования инженерного мышления слушателей и курсантов Уральского института ГПС МЧС РФ и структурно состоит из двух частей: 1-я – теоретическая механика,

2-я – сопротивление материалов.

В первой части курса «Прикладная механика» слушатели изучают теоретическую механику, которая структурно состоит из трех разделов: статика, кинематика и динамика.

При изучении теоретической механики следует пользоваться тематическим планом курса, приведенном в рабочей программе курса. В этом плане указаны параграфы рекомендуемого учебника, в котором освещены все вопросы курса, подлежащие изучению. В соответствии с программой слушатели выполняют две контрольные расчетно-графические работы по соответствующим разделам теоретической механики.

Для изучения курса необходимо иметь соответствующую математическую подготовку. Во всех разделах, начиная со статики, широко используется векторная алгебра. Необходимо уметь вычислять проекции векторов на координатные оси, находить геометрически (построением векторного треугольника или многоугольника) и аналитически (по проекциям на координатные оси) сумму векторов, вычислять скалярное и векторное произведение двух векторов и знать свойства их произведений, в кинематике и динамике – дифференцировать векторы. Надо также уметь свободно пользоваться системой прямоугольных декартовых координат на плоскости и в пространстве, знать, что такое единичные векторы (орты) этих осей и как выражаются составляющие вектора по координатным осям с помощью ортов.

Для изучения кинематики надо совершенно свободно уметь дифференцировать функции одного переменного, строить графики этих функций, быть знакомым с понятиями о естественном трехграннике, кривизне кривой и радиусе кривизны, знать основы теории кривых второго порядка, изучаемой в аналитической геометрии

Для изучения динамики надо уметь находить интегралы (неопределенные и определенные) от простейших функций и вычислять частные производные.

Изучать материал рекомендуется по главам (параграфам) рекомендованного учебника. Сначала следует прочитать весь материал темы (параграфа), особенно не задерживаясь на том, что показалось не совсем понятным; часто это становится понятным из последующего. Затем надо вернуться к местам, вызвавшим затруднения, и внимательно разобраться в том, что было неясно. Особое внимание при повторном чтении обратите на формулировки соответствующих определений, теорем и т.п. (они обычно бывают набраны в учебнике курсивом или разрядкой); в точных формулировках, как правило, бывает существенно слово, и очень полезно понять, почему данное положение сформулировано именно так. Однако не следует стараться заучивать формулировки; важно понять их смысл и уметь изложить его своими словами.

Убедившись, что теоретический материал усвоен, переходите к решению задач, предварительно разобрав приведенные в учебнике примеры. Для закрепления материала курса и приобретения практических навыков следует решить рекомендованные в тематическом плане курса задачи.

Каждую контрольную работу необходимо выполнять на листах бумаги формата А-4, чернилами (не красными), четким почерком с полями 40 мм с левой стороны страницы для замечаний рецензента. В конце решения каждой задачи оставлять чистый лист для указаний рецензента. Титульный лист каждой работы оформляется по утвержденной в Институте форме (Приложение1).

Допускается оформление контрольной работы в печатном и в электронном вариантах (с предоставлением дискеты). Для электронной версии формат файла – Microsoft Word, параметры шрифта – Times New Roman, кегль 14, интервал 1,0.

Выполняя контрольные работы, необходимо полностью переписать текст каждой задачи и карандашом аккуратно сделать соответствующий чертеж, на котором указываются численные значения заданных величин.

Расчетные схемы и числовые данные каждой задачи выбираются в соответствии с учебным шифром, определяемым тремя последними цифрами номера зачетной книжки слушателя. По цифрам шифра определяются строки, а порядковые номера цифр в шифре определяют столбцы в таблице с данными задачи. На пересечении соответствующих строк и столбцов определяются условия для индивидуального варианта задачи.

Например, для учебного шифра 386 из таблицы 1 для решения задачи следует взять: условие №1, схема VI (по рис. 1), углы =75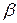⁰, =45⁰, 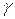=45⁰, сила Q=300 Н.

Работы, выполненные с нарушением этих указаний, не проверяются и не зачитываются.

Решение каждой задачи должно сопровождаться кратким пояснением, т.е. надо указывать, какие формулы или уравнения применяются для ее решения. Все этапы решения задачи нумеруются в соответствии с пунктами методических указаний и снабжаются краткими и четкими пояснениями.

При расчетах вначале выписывается используемая формула с применением общепринятых буквенных обозначений, затем подставляются исходные цифровые значения вместо буквенных в той же последовательности, и только после этого производятся требуемые математические операции. Все расчеты в контрольных работах следует производить с помощью микрокалькулятора. Окончательные результаты с обязательным указанием размерности выделяются (подчеркиваются или берутся в рамки). Рекомендуется производить оценку правдоподобности окончательных результатов с точки зрения их физической сущности и исходных данных.

Все задания контрольных работ составлены в Международной системе единиц (СИ), основные и некоторые производные единицы которой приведены в таблице П 1 приложения. При слишком больших или слишком малых числах в вычислениях по Международной системе рекомендуется пользоваться кратными или дольными единицами, приведенными в таблице П 2 приложения.

Кратные и дольные единицы измерения образуются добавлением приставок к корневой части названий единиц, например; сантиметр (см), кубический дециметр (дсм³), меганьютон (МН), киловатт (кВт). Для производных единиц, составленных из наименований нескольких единиц, приставка добавляется только к первой по порядку единице, например, килоньютон-метр (кН×м).

Задача 1. Равновесие тела под действием сходящейся системы сил

Условие №1. На конструкции, состоящей из двух невесомых стержней AB и AC, скрепленных между собой и с опорами при помощи шарниров, укреплен в узле А блок. Через блок перекинут невесомый канат, один конец которого прикреплён в точке D, а к другому подвешен груз Q. Определить усилия в стержнях, пренебрегая размерами блока. Задачу решить аналитическим и геометрическим способами.

Условие №2. Определить давление однородного шара весом Q на опоры, если шар опирается в схемах VII – VIII на две гладкие плоскости, в схеме IX – на плоскость и выступ, в схеме X – на два выступа. Задачу решить аналитическим и геометрическим способами.

Схемы к задаче приведены на рис. 1, численные данные – в табл. 1.

Таблица 1

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра
номер условия	номер схемы	углы, град	Q, Н
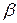
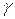
		I
		II
		III
		IV
		V
		VI
		VII
		VIII
		IX
		X

Рис. 1
Пример выполнения задачи 1

Задача 1 относится к равновесию плоской системы сходящихся сил. Для её решения необходимо рассмотреть равновесие сил, приложенных к телу (блок в условии №1 или шар в условии №2). К телу, освобожденному от связей, следует приложить как активные силы, так и силы реакций связей. Чтобы найти искомые величины, необходимо составить уравнения равновесия.

В качестве примера решим задачу 1 по варианту, соответствующему условному шифру 000. Для этого шифра, все цифры которого одинаковы и равны 0, из последней строки таблицы 1 принимаем: условие №2, схема X, углы 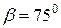и 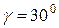, силу Q =1000 Н.

1. К шару приложена система трех сходящихся сил 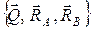(рис. 1.1, а). Перенесем точки приложения сил реакций 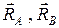в точку О и проведем через нее ось х, направленную по линии действия реакции и, ось y, перпендикулярно ей (рис. 1.1, б).

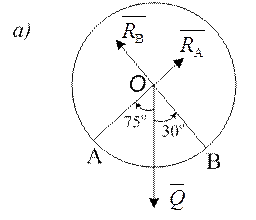
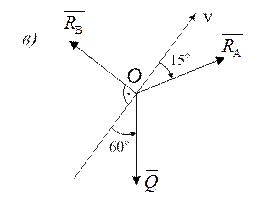
Рис. 1.1.

Составим уравнения равновесия в виде суммы проекций всех сил системы на ось u и решим его.

, ;

.

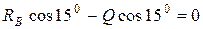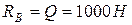Проведем через точку О другую ось v, перпендикулярную линии действия силы 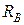(рис. 1.1, в)

Составим уравнение равновесия для данной системы сил 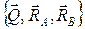в виде суммы всех сил на ось v и решим его.

.

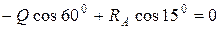
2. Для проверки решим задачу геометрическим способом. Через конец и начало вектора заданной силы 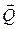проведем линии, параллельные направлениям искомых сил реакций связей и . Получим замкнутый силовой треугольник (рис. 1.1, г). Запишем соотношение теоремы синусов для этого треугольника 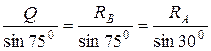, из которого найдем

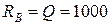, Н;

, Н.

Задача 2. Равновесие тела под действием плоской системы сил

На горизонтальную балку пролетом AB = l действует сосредоточенная сила 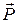, пара сил с моментом m и равномерно распределённая нагрузка интенсивностью q. Определить реакции опор в точках A и B, пренебрегая весом балки и стержня BC.

Схемы к задаче приведены на рис. 2, численные данные – в табл. 2.

Таблица 2

Цифры шифра	3-я цифра шифра	2-я цифра шифра	1-я цифра шифра	2-я цифра шифра
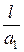
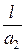
номер схемы	l, м			углы, град
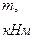
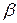
	I
	II
	III
	IV
	V
	VI
	VII
	VIII
	IX
	X

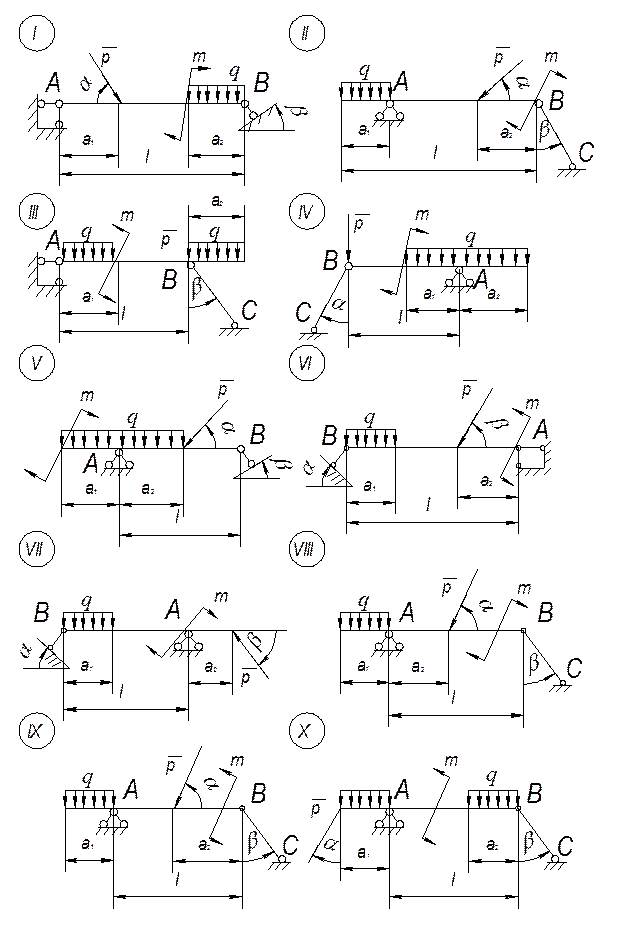
Рис. 2

Дата добавления: 2014-12-08