
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример выполнения задачи 5
|
|
|
|
Задача 5 относится к кинематике точки. Для определения скорости и ускорения точки следует определить их проекции на координатные оси. Зная  и
и 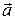 , найти касательное и нормальное ускорение точки, а также радиус кривизны траектории.
, найти касательное и нормальное ускорение точки, а также радиус кривизны траектории.
В качестве примера решим задачу 5 по варианту, соответствующему условному шифру 000. По таблице 5 принимаем уравнение движения точки в декартовых координатах:  ,
, 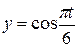 ,
,  ,
, 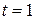 с.
с.
1. Определим проекции скорости на оси декартовой системы координат в данный момент времени 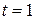 с.
с.
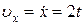 ,
,  см/с;
см/с;
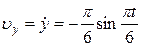 ,
, 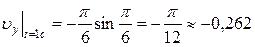 см/с;
см/с;
 ,
,
 см/с.
см/с.
2. Модуль скорости точки в данный момент времени равен
 см/с.
см/с.
3. Направление вектора скорости в данный момент определяется углами
 (14,60),
(14,60),
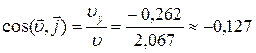 (97,30),
(97,30),
 (102,70).
(102,70).
4. Определим проекции ускорения на оси декартовой системы координат в данный момент времени 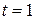 с.
с.
 ,
, 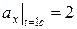 см/с2;
см/с2;
 ,
, 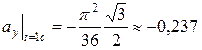 см/с2;
см/с2;
 ,
,
 см/с2.
см/с2.
5. Модуль ускорения точки в данный момент времени равен
 см/с2.
см/с2.
6. Направление вектора ускорения в данный момент определяется углами
 (10,20),
(10,20),
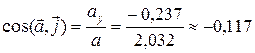 (96,70),
(96,70),
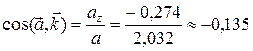 (97,70).
(97,70).
7. Радиус кривизны траектории 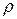 определим из формулы
определим из формулы  , где
, где 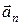 – проекция ускорения на нормаль (нормальное ускорение точки).
– проекция ускорения на нормаль (нормальное ускорение точки). 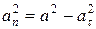 , где
, где  – проекция ускорения на касательную (касательное ускорение точки)
– проекция ускорения на касательную (касательное ускорение точки)
 .
.
В данный момент времени касательное ускорение точки равно
 см/с2,
см/с2,
а радиус кривизны траектории равен
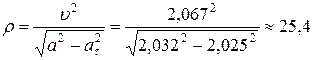 см.
см.
Задача 6. Вращение твердого тела вокруг неподвижной оси
Условие №1. По заданному уравнению вращательного движения твердого тела вокруг неподвижной оси  определить:
определить:
1) угловую скорость и угловое ускорение тела в момент времени  ;
;
2) скорость и ускорение точки тела, отстоящей на расстоянии  от оси, в момент времени
от оси, в момент времени  ;
;
3) число оборотов  тела за время
тела за время  .
.
Условие №2. Диск, вращающийся равноускоренно вокруг неподвижной оси, в моменты  и
и  имеет угловые скорости
имеет угловые скорости  и
и  соответственно. Определить:
соответственно. Определить:
1) скорость и ускорение точки тела, отстоящей на расстоянии  от оси, в момент времени
от оси, в момент времени  ;
;
2) число оборотов  тела за время
тела за время  ;
;
3) уравнение вращательного движения диска, если при  =0,
=0, 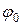 =0.
=0.
Условие №3. Тело, вращаясь равноускоренно с угловым ускорением 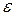 , имеет в момент времени
, имеет в момент времени  угловую скорость
угловую скорость  . Определить:
. Определить:
1) скорость и ускорение точки тела, отстоящей на расстоянии  от оси, в момент времени
от оси, в момент времени  ;
;
2) число оборотов  тела за время
тела за время  ;
;
3) уравнение вращательного движения тела, если при  =0,
=0, 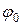 =0.
=0.
Численные данные приведены в табл. 6.
Таблица 6
| Цифры шифра | 3-я цифра шифра | 2-я цифра шифра | 1-я цифра шифра | ||||||
| Номер условия |  ,
рад ,
рад
|  , ,

|  , ,

| 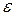 , ,
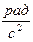
|  , с , с
|  , с , с
|  , с , с
|  , см , см
| |
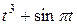
| - | - | - | 0,5 | |||||
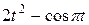
| - | - | - | 1,0 | |||||

| - | - | - | 1,5 | |||||
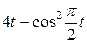
| - | - | - | 2,0 | |||||
| - | - | 2,5 | |||||||
| - | - | 0,5 | |||||||
| - | - | 1,0 | |||||||
| - | - | 1,0 | 1,5 | ||||||
| - | - | 1,5 | 2,0 | ||||||
| - | - | 2,0 | 2,5 |
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 433; Нарушение авторских прав?; Мы поможем в написании вашей работы!