
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач Т1 1 страница
|
|
|
|
Основные разделы курса и вопросы для самоконтроля
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Литература по Сопротивлению материалов
1. Степин П.А. Сопротивление материалов / П.А. Степин. – Москва: Высш. шк., 1988. – 368 с.
2. Александров А.В. Сопротивление материалов / А.В.Александров, В.Н. Трошин, В.И. Шалашилин. - Москва: Высш. шк., 2001. – 560 с.
3. Горшков А.Г. Сопротивление материалов / А.Г. Горшков,
В.Д. Потапов, Б.П. Державин. – Москва: Физматлит, 2002. – 560 с.
4. Миролюбов И.Н. Сопротивление материалов: пособие по решению задач / И.Н. Миролюбов. 8-е изд. стер. – Санкт-Петербург: “Лань”, 2009. – 512 с.
5. Ицкович Г.М. Сопротивление материалов: учебник / Г.М. Ицкович. – 7-е изд., испр. – Москва: Высш. шк., 1986. – 352 с.
Теория механизмов и машин – наука, изучающая общие методы структурного и динамического анализа и синтеза различных механизмов, механику машин. Важно подчеркнуть, что излагаемые в теории механизмов и машин методы пригодны для проектирования любого механизма и не зависят от его технического назначения, а также физической природы рабочего процесса машины.
Курс теории механизмов и машин (по существу) является вводным в специальность будущего инженера и поэтому имеет инженерную направленность; в нем широко используется современный математический аппарат и изучаются практические приемы решения задач анализа и синтеза механизмов – аналитические с применением ЭВМ, графические и графоаналитические.
Структура механизмов
1. Приведите определение звена, кинематической пары, кинематической цепи. 2. Назовите основные плоские кинематические пары, объясните деление пар на высшие и низшие, покажите возможные и невозможные движения звеньев пар относительно друг друга. Приведите пример пространственной пары. 3. Какие кинематические цепи, замкнутые или незамкнутые, используют обычно для механизмов? Приведите определение механизма. 4. Объясните физический смысл числовых коэффициентов в структурной формуле. Почему большинство механизмов должно иметь одну степень свободы? Можно ли в механизме с одной степенью свободы изменить положение звеньев, не меняя положения входного звена? 5. Приведите пример пространственного механизма и покажите на нем движения звеньев, отличающие его от плоского механизма.
Анализ механизмов
1. Через планы положений кривошипно-ползунного механизма, шарнирного четырехзвенника и кулисного механизма определите крайние положения ведомого звена. 2. Напишите векторные уравнения: связывающее скорости двух точек одного звена и связывающее их ускорения. 3. Постройте план скоростей и план ускорений для шарнирного четырехзвенника и определите числовое значение угловой скорости и углового ускорения шатуна и их направление. Как следует определять скорость (ускорение) третьей точки звена при известных векторах скоростей (ускорений) двух точек этого звена, используя свойство подобия? 4. Как по кривой диаграммы перемещений звена определить положения механизма, при которых скорость звена равна нулю, и положения, при которых скорость максимальна? 5. Какие виды сил могут действовать на механизм при его движении? Могут ли силы трения быть движущими силами? 6. Как ставится задача кинетостатического анализа: что известно и что нужно найти? 7. На каком основании в кинетостатическом анализе приравнивают нулю сумму сил и сумму моментов, действующих на звенья движущегося механизма? 8. Какими способами можно определить уравновешивающий момент на кривошипе? Зависит ли он от скорости движения? 9. Как применить рычаг Жуковского для определения приведенной силы? 10. Почему приведенная масса (или приведенный момент инерции) рычажного механизма изменяется с изменением его положения, а для зубчатого механизма постоянна? Меняется ли приведенная масса с изменением скорости? 11. Какое уравнение движения (уравнение кинетической энергии или дифференциальное уравнение движения) следует применять для определения закона движения механизма для случаев: силы - функция положения, силы – функция скорости? 12. Как можно уменьшить время разбега и выбега? Изменяется ли кинетическая энергия на режиме установившегося движения? 13. Что такое средняя скорость установившегося движения, коэффициент неравномерности движения? 14. Что такое неуравновешенность? Через какие места вращающаяся масса воздействует на стойку? Каковы вредные последствия неуравновешенности вообще и когда неуравновешенность особенно опасна? 15. Что такое статическая балансировка, гарантирует ли она полное уравновешивание, сколько уравновешивающих грузов достаточно для статического уравновешивания? 16. Сколько уравновешивающих грузов достаточно для полного уравновешивания вращающейся массы?
Синтез механизмов
1. При каких соотношениях между размерами звеньев кривошип в дезаксиальном кривошипно-ползунном механизме не сможет совершить полный оборот (станет коромыслом)? 2. Спроектируйте кривошипно-коромысловый шарнирный четырехзвенник по двум заданным крайним положениям его коромысла. 3. Как определяют общее передаточное отношение длясоединения зубчатых колес с неподвижными осями вращения промежуточными двойными и одиночными колесами? Что означают знаки «+» и «–» в передаточных отношениях? Для чего применяют сложные соединения зубчатых колес? 4. По формуле передаточного отношения планетарной передачи покажите, что планетарная передача может иметь большее передаточное отношение, чем передача с неподвижными осями, составленная из тех же колес. 5. Каковы требования к положению общей нормали к профилям зубьев для получения постоянного передаточного отношения? Какова форма зубчатых колес с переменным передаточным отношением? 6. По модулю и числу зубьев найдите параметры нормального зубчатого колеса: радиусы или диаметры четырех характерных окружностей, шаг, толщину зуба и ширину впадины. Что такое эвольвента, как ее построить, каковы ее свойства и какая часть зуба очерчивается по эвольвенте? 7. Определите общие параметры нормальных колес, находящихся во внешнем зацеплении: начальные окружности, полюс зацепления, межосевое расстояние, угол зацепления, линий зацепления, рабочие участи профилей, угол перекрытия, коэффициент перекрытия. Покажите, что передаточное отношение при движении работающих зубьев остается постоянным. Будет ли в эвольвентном зацеплении изменяться скорость ведомого колеса, если при постоянной скорости ведущего колеса «на ходу» несколько изменять межосевое расстояние? 8. Почему желательно применение колес с малым числом зубьев и что препятствует в этом случае применению нормальных колес? 9. Для каких целей применяют корригированные колеса и какими размерами они отличаются от нормальных колес того же модуля и числа зубьев? 10. Почему в передаточное отношение пространственной передачи не вводят знак, характеризующий связь между направлениями вращений? 11. Определите передаточное отношение конической зубчатой передачи через углы начальных конусов. В каком месте конического колеса модуль стандартный? 12. Как определить передаточное отношение червячной передачи? 13. Начертите схемы распространенных типов плоских и пространственных кулачковых механизмов. 14. Как по чертежу кулачкового механизма получить диаграмму перемещений ведомого звена? 15. Сравните кулачковые и рычажные механизмы по их достоинствам и недостаткам.
Основы теории машин-автоматов
1. Каковы недостатки системы управления с кулачковым рас- пределительным валом? 2. В чем удобство применения в автоматике двоичной системы счисления? 3. Назовите основные логические опе- рации и объясните работу соответствующих логических элементов, выполняющих эти операции. 4. В чем удобство применения системы управления по пути (от сигналов конечных выключателей) по сравнению с системой управления по времени (от кулачкового вала) 5. Назовите условия работы, в которых применение манипуляторов особенно необходимо. 6. Для каких работ применяют промышленных роботов? 7. Почему для манипуляторов и роботов необходимы кинематические цепи со многими степенями свободы?
2.2. Задачи по «Теории механизмов и машин»
Контрольная работа по «Теории механизмов и машин» состоит из двух задач. Номер варианта схемы механизма студент выбирает по последней цифре своего шифра (если эта цифра 0, то выполняют вариант 10), а числовые данные – из соответствующей таблицы по предпоследней цифре шифра.
Задача Т1
В зубчатой передаче, показанных на схемах (рис. 9 – 18), входное колесо 1 в данный момент имеет угловую скорость 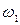 и постоянное угловое ускорение
и постоянное угловое ускорение 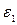 , направленное по движению или против движения. Определить:
, направленное по движению или против движения. Определить:
1) передаточное отношение между входным и выходным звеньями и его знак (если их оси вращения параллельны);
2) угловую скорость и угловое ускорение выходного звена, их направления показать на схеме передачи;
3) время, в течение которого угловая скорость увеличится в два раза (если движение ускоренное), или уменьшится до нуля (если движение замедленное);
4) общий коэффициент полезного действия передачи.
В таблице заданных величин z – число зубьев колес приводится с индексом, соответствующим их номеру на схеме механизма, для червяка 1; 2; 3 г – число заходов, а направление витков червяка указано буквами: л – левое, п – правое.
Для расчетов принять следующие значения коэффициента полезного действия (учитывающего потери и в зацеплении и в подшипниках): для пары цилиндрических колес 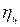 =0,97; для пары конических колес
=0,97; для пары конических колес 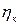 =0,95; для планетарной передачи с внешними зацеплениями ее колес
=0,95; для планетарной передачи с внешними зацеплениями ее колес 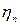 =0,5, а для имеющей внутреннее зацепление одной из пар
=0,5, а для имеющей внутреннее зацепление одной из пар 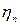 = 0,96; для червячной передачи при одно-, двух- и трехзаходном червяке – соответственно
= 0,96; для червячной передачи при одно-, двух- и трехзаходном червяке – соответственно 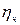 =0,7; 0,75; 0,8.
=0,7; 0,75; 0,8.
Вариант 1 (рис. 9, табл. 7)
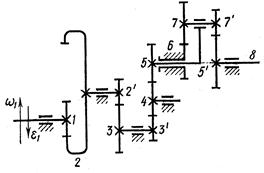 Рис. 9
Рис. 9
| Вариант 2 (рис.10, табл. 8)
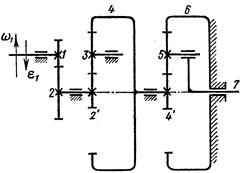 Рис. 10
Рис. 10
|
Таблица 7
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ | ||||||||||
| Z3 | ||||||||||
| Z3’ | ||||||||||
| Z5 | ||||||||||
| Z6 | ||||||||||
| Z7 | ||||||||||
| Z7’ | ||||||||||
| Z8 | ||||||||||
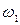 , рад/с , рад/с
| ||||||||||
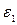 , рад/с2 , рад/с2
|
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’, Z4’ | ||||||||||
| Z3 , Z5 | ||||||||||
| Z4 , Z6 | ||||||||||
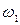 , рад /с , рад /с
| ||||||||||
 , рад/с2 , рад/с2
|
Таблица 8
Вариант 3 (рис. 11, табл. 9)
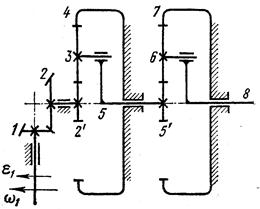 Рис. 11
Рис. 11
| Вариант 4 (рис.12, табл. 10)
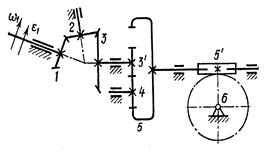 Рис. 12
Рис. 12
|
Таблица 9
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ , Z5’ | ||||||||||
| Z3,Z6 | ||||||||||
| Z4,Z7 | ||||||||||
 , рад/с , рад/с
| ||||||||||
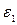 , рад/с2 , рад/с2
|
Таблица 10
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z3 | ||||||||||
| Z3’ | ||||||||||
| Z5 | ||||||||||
| Z5’ | 3, п | 2, л | 1, п | 2, л | 1,п | 3, л | 2,п | 1.л | 2,п | 3,л |
| Z6 | ||||||||||
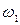 , рад/с , рад/с
| ||||||||||
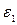 , рад/с2 , рад/с2
|
Вариант 5 (рис. 13, табл. 11)
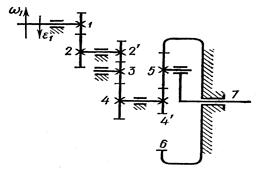 Рис. 13
Рис. 13
| Вариант 6 (рис.14, табл. 12)
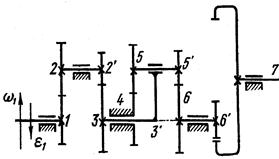 Рис. 14
Рис. 14
|
Таблица 11
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ | ||||||||||
| Z4 | ||||||||||
| Z4’ | ||||||||||
| Z5 | ||||||||||
| Z6 | ||||||||||
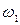 , рад/с , рад/с
| ||||||||||
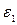 , рад/с2 , рад/с2
|
Таблица 12
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ | ||||||||||
| Z3 | ||||||||||
| Z4 | ||||||||||
| Z5 | ||||||||||
| Z5’ | ||||||||||
| Z6 | ||||||||||
| Z6’ | ||||||||||
| Z7 | ||||||||||
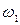 , рад/с , рад/с
| ||||||||||
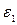 , рад /с2 , рад /с2
|
Вариант 7 (рис. 15, табл. 13)
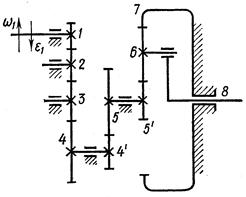 Рис. 15
Рис. 15
| Вариант 8 (рис.16, табл. 14)
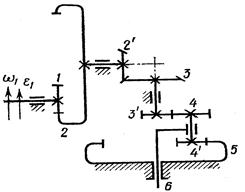 Рис. 16
Рис. 16
|
Таблица 13
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z4 | ||||||||||
| Z4’ | ||||||||||
| Z5 | ||||||||||
| Z5’ | ||||||||||
| Z6 | ||||||||||
| Z7 | ||||||||||
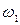 , рад /с , рад /с
| ||||||||||
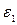 , рад/с2 , рад/с2
|
Таблица 14
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ | ||||||||||
| Z3 | ||||||||||
| Z3’ | ||||||||||
| Z4 | ||||||||||
| Z4’ | ||||||||||
| Z5 | ||||||||||
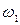 , рад/с , рад/с
| ||||||||||
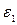 , рад /с2 , рад /с2
|
Вариант 9 (рис. 17, табл. 15)
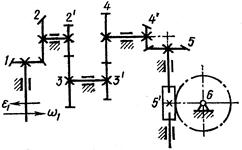 Рис. 17
Рис. 17
| Вариант 10 (рис.18, табл. 16)
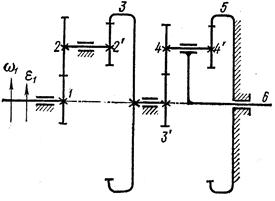 Рис. 18
Рис. 18
|
Таблица 15
| Величина | Предпоследняя цифра шифра | |||||||||
| Z1 | ||||||||||
| Z2 | ||||||||||
| Z2’ | ||||||||||
| Z3 | ||||||||||
| Z3’ | ||||||||||
| Z4 | ||||||||||
| Z4’ | ||||||||||
| Z5 | ||||||||||
| Z5’ | 2, л | 3, п | 2, л | 1,п | 3, л | 2,п | 1,л | 3, п | 2, л | 1, п |
| Z6 | ||||||||||
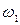 , рад/с , рад/с
| ||||||||||
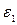 , рад/с2 , рад/с2
|
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 3416; Нарушение авторских прав?; Мы поможем в написании вашей работы!