Общие условия равновесия

Любая закрытая система, находящаяся в равновесии при постоянных давлении и температуре, характеризуется соотношением: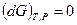

Для системы переменного состава (смотри (III, 58)):

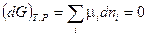(IV, 11)

Если при постоянных Р и Т из фазы 1 в фазу 2 переходит 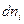молей i - ого компонента, то

(IV, 12),

где верхний индекс относится к фазе, а нижний индекс — к компоненту.

При переходе dn_i молей i - ого компонента из фазы 1 в фазу 2 его количество в одной из фаз убывает, а в другой фазе увеличивается на ту же самую величину, следовательно, . Тогда уравнение (IV, 12) можно записать в следующем виде:

или 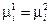(IV, 13)

Таким образом, химический потенциал i - ого компонента в фазе 1 равен химическому потенциалу в фазе 2.

Обобщая этот результат на все фазы и все компоненты гетерогенной системы, получим условие равновесия:

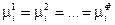(IV, 14),

где Ф — число фаз.

Таким образом, гетерогенная система будет находиться в состоянии равновесия при выполнении равенств (IV, 14) и ряда тождеств:

T ¹ = T ² =... = T^Ф = T

P ¹ = P ² =... = P^Ф = P

Покажем, что равенство интенсивных переменных — температур, давлений и химических потенциалов компонентов есть также условие равновесия в изолированных системах, что непосредственно вытекает из второго закона термодинамики.

Воспользуемся обобщенной формой записи первого и второго законов термодинамики (смотри (III, 63)):

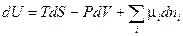
Перепишем это уравнение относительно dS:

(IV, 15)

Из этого уравнения следует, что частные производные энтропии по экстенсивным переменным U,V и n_i выражаются через интенсивные свойства системы Т, Р и m _i:

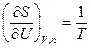(IV, 16)

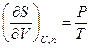
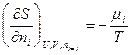
Рассмотрим изолированную систему, состоящую из двух подсистем «А» и «В», открытых по отношению друг к другу (смотри рис.14).

Рис. 14. Изолированная система, состоящая из двух подсистем, открытых по отношению друг к другу.

Эти подсистемы способны обмениваться энергией и веществом, но оболочка, ограничивающая систему в целом, остается несжимаемой и исключает теплообмен. Внутренняя энергия, энтропия, объем и количества компонентов — функции экстенсивные. Поэтому для изолированной системы, состоящей из «А» и «В», справедливы следующие соотношения:

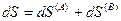(IV, 17)

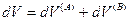
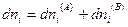
и поскольку U,V и n всей системы имеют постоянные значения (изолированная система), то

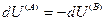(IV, 18)

Энтропия — внутреннее свойство термодинамической системы; согласно постулатам термодинамики, при равновесии она является функцией внутренней энергии и внешних переменных.

Если в качестве внешних переменных для каждой из подсистем «А» и «В» выбрать их объем и количества веществ, то полный дифференциал функции S = S (U,V,n) для каждой из подсистем запишется в виде (IV, 15), а частные производные будут выражены формулами (IV, 16).

С учетом этого и соотношений (IV, 18) общее изменение энтропии изолированной системы запишется следующим образом:

Согласно второму закону термодинамики, при равновесии энтропия изолированной системы достигает максимума, т. е. dS_U,V,n = 0. Изменения dU^A, dV^A и 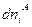являются независимыми, поэтому равенство нулю dS_U,V,n возможно только в том случае, если равен нулю каждый из коэффициентов, стоящих в квадратных скобках, т. е.

Если теперь принять во внимание выражения для частных производных энтропии (смотри (IV, 16)), то получим следующие соотношения:

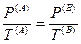
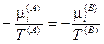
Из последних трех уравнений очевидным образом следуют общие условия равновесия изолированной термодинамической системы:

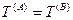— термическое равновесие,

— механическое равновесие,

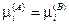— химическое равновесие.

Если хотя бы некоторые из этих условий не выполняются, то система является неравновесной и в ней могут происходить процессы, сопровождающиеся выравниванием соответствующих интенсивных параметров.

Дата добавления: 2014-11-29