Фазовые переходы второго рода

Фазовый переход второго рода — это равновесный переход вещества из одной фазы в другую, при котором скачкообразно изменяются только вторые производные от энергии Гиббса по температуре и давлению.

В частности, из уравнения (III, 32) следует, что:

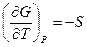
Следовательно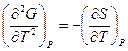

В соответствии с уравнением (II, 31) можно записать:

, тогда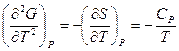

Таким образом, вторая производная G по температуре, равная отношению теплоемкости при постоянном давлении к температуре, при фазовом переходе второго рода будет изменяться скачкообразно, как и другие вторые производные энергии Гиббса.

Примерами фазовых переходов второго рода являются переходы жидкого гелия в сверхтекучее состояние, железа из ферромагнитного в парамагнитное состояние (так называемая точка Кюри), металлов в сверхпроводящее состояние, взаимные переходы изомеров и т. д.

Рассмотрим более подробно такое аномальное поведение эквимольного сплава меди и золота около некоторой температуры (Т ~ 710 К).

Именно в этой точке теплоемкость сплава изменяется скачкообразно. Вид кривой зависимости 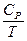от абсолютной температуры показан на рис.10.

Рис. 10. Кривая зависимости 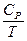от абсолютной температуры
эквимольного сплава меди и золота.

Пик, изображенный на рисунке, напоминает греческую букву λ (лямбда), поэтому точку, соответствующую максимуму по температурной шкале, называют лямбда — точкой. Природа такого изменения теплоемкости в случае сплава меди и золота связана с изменением его внутреннего строения (конфигурации) — с исчезновением так называемого дальнего порядка (трансляционной симметрии), при котором атомы меди и золота в кристаллической решетке образуют как бы проникающие друг в друга подрешетки.

При фазовых переходах второго рода сама энергия Гиббса изменяется непрерывно с изменением термодинамических параметров (смотри рис.11).

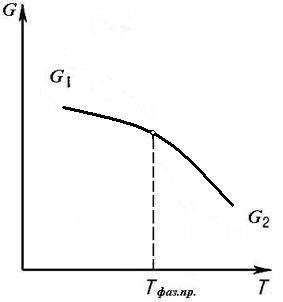
Рис. 11. Зависимость энергии Гиббса системы от температуры при фазовом переходе второго рода.

При фазовых переходах второго рода непрерывно изменяются не только энергия Гиббса, но и первые производные от энергии Гиббса по температуре и давлению, т. е. энтропия и объем.

В системах с фазовыми переходами второго рода невозможно существование метастабильных состояний.

Дата добавления: 2014-11-29