Химический потенциал

Чтобы прояснить смысл понятия «химический потенциал», продифференцируем выражение (III,51) как произведение при постоянных Р и Т:

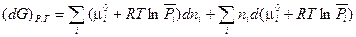(III, 57)

Легко показать, что при постоянных Р и Т второе слагаемое 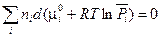( 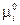зависит только от температуры).

Тогда для системы переменного состава

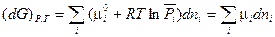(III, 58)

Примем постоянным число молей всех компонентов смеси, кроме i - ого компонента, тогда

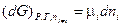(III, 59)

или

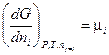(III, 60)

Из определения химического потенциала как частной производной вытекает следующее. Если при постоянных температуре Т и давлении Р к бесконечно большому количеству смеси (раствора) определенного состава добавить один моль какого-нибудь компонента, то химический потенциал будет равен приросту энергии Гиббса.

Сказанное выше позволяет определить химический потенциал как энергию Гиббса, приходящуюся на один моль компонента в смеси или, иными словами, парциальную молярную энергию Гиббса.

Полный дифференциал энергии Гиббса в соответствии с (III, 31) и (III, 59) запишется следующим образом:

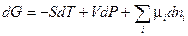(III, 61)

Исходя из этого выражения, можно показать, что для систем с переменным составом фундаментальные термодинамические уравнения будут иметь следующий вид:

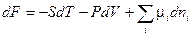(III, 62)

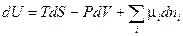(III, 63)

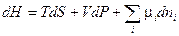(III, 64)

Из уравнений (III, 61) — (III, 64) вытекает:

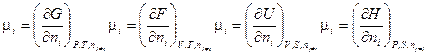
Таким образом, химический потенциал является частной производной по количеству i - ого компонента от любой характеристической функции G,F,U и H при постоянном количестве остальных индивидуальных веществ в системе и постоянстве соответствующих естественных переменных.

Необходимо отметить, что химический потенциал является интенсивным свойством системы.

Химический потенциал одного моля индивидуального вещества в состоянии идеального газа при любых температуре Т и давлении Р можно рассчитать по уравнению:

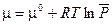(III, 65)

Вообще химический потенциал индивидуального вещества — это мольная энергия Гиббса: 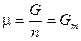, где G_m — энергия Гиббса 1 моля индивидуального вещества.

Для практических целей широко используют мольную энергию Гиббса в стандартном состоянии (при 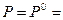1 атм. и Т = 298 К).

В этом случае

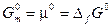
Величину, которую мы обозначили 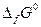, также определяют как стандартную молярную энергию Гиббса образования одного моля вещества из простых веществ, находящихся в их стандартных состояниях.

При этом полагают, что энергия Гиббса образования (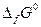) всех элементов при всех температурах равна нулю.

Стандартные энергии Гиббса образования многих соединений табулированы. По взятым из таблиц значениям 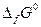может быть рассчитано изменение энергии Гиббса химической реакции аналогично тому, как рассчитывается тепловой эффект химической реакции по значениям стандартных теплот образования веществ, участвующих в химической реакции.

ГЛАВА IV.
ПРИМЕНЕНИЕ ЭНЕРГИИ ГИББСА К ИЗУЧЕНИЮ ФАЗОВЫХ РАВНОВЕСИЙ

Вещества, образующие термодинамическую систему, могут находиться в различных агрегатных состояниях: газообразном, жидком, твердом. Жидкие и твердые фазы называются конденсированными.

Напомним определение фазы. Гомогенные части системы, отделенные от остальных частей видимыми поверхностями раздела, называются фазами. При этом совокупность отдельных гомогенных частей системы, обладающих одинаковыми физическими и термодинамическими свойствами, считается одной фазой (например, совокупность кристаллов одного вещества или совокупность капелек жидкости, взвешенных в газе и составляющих туман).

По числу фаз системы делятся на однофазные, двухфазные, трехфазные и многофазные.

Каждая фаза состоит из одного или нескольких веществ. Индивидуальные химические вещества, которые могут быть выделены из системы простыми препаративными методами (кристаллизация, испарение, осаждение и т. д.) и существовать вне ее самостоятельно, называются составляющими веществами системы.

Составляющие вещества, наименьшее число которых необходимо для однозначного определения состава каждой фазы при любых условиях существования системы, называются компонентами.

Если в системе между составляющими веществами нет химического взаимодействия, то число компонентов равно количеству составляющих веществ. При химическом взаимодействии в системе число компонентов находится как разность между числом составляющих веществ системы и числом уравнений, связывающих равновесные концентрации этих веществ. В этом случае в качестве компонентов могут быть выбраны любые составляющие вещества, т. к. свойства системы определяются не тем, какие составляющие вещества выбраны в качестве компонентов, а их числом, т. е. числом компонентов.

Следовательно, число компонентов или совпадает с числом составляющих веществ (при отсутствии химических реакций), или меньше его. Но даже в этом случае число компонентов — величина вполне определенная, зависящая от свойств системы.

Число независимых термодинамических параметров состояния фаз равновесной системы, произвольное изменение которых в определенных пределах не вызывает исчезновения одних и образования других фаз (т. е., не вызывает изменения фазового состава системы), называется числом термодинамических степеней свободы или вариантностью системы. По числу термодинамических степеней свободы (С) системы подразделяются на инвариантные (С = 0), моновариантные (С = 1) и т. д.

Дата добавления: 2014-11-29