Соотношения Максвелла

Рассмотрим теперь вторые смешанные производные характеристических функций. Принимая во внимание уравнения (III, 26), можем записать:

( III, 33 )

( III, 34 )

Значение смешанных производных непрерывной функции не зависит от порядка дифференцирования, поэтому, если в уравнениях ( III,33 ) и ( III,34 ) равны левые части уравнений, то равны и их правые части:

Справедливость полученного уравнения не изменится, если его «перевернуть», т. е. представить в следующем виде:

( III, 35 )

Полученное уравнение (III, 35) принадлежит к числу так называемых соотношений Максвелла. Совершенно аналогично (смотри (III, 28), (III, 30) и (III, 32)) можно получить три других соотношения:

или

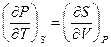( III, 36 )

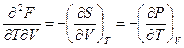или

( III, 37 )

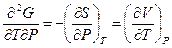или

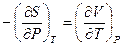( III, 38 )

Эти соотношения позволяют при необходимости переходить от одних частных производных к другим, заменяя частные производные, которые не могут быть непосредственно определены на опыте (производные энтропии по параметрам Р и V) на величины, которые заведомо легче связать с экспериментом (производные давления или объема по температуре и другие). Поэтому роль соотношений Максвелла, особенно

( III,37 ) и ( III,38 ), в термодинамике чрезвычайно велика.

Приведем только один пример. Из объединенного первого и второго законов термодинамики следует:

TdS = dU + PdV

Если разделить обе части последнего уравнения на dV, считая температуру Т постоянной, получим:

Заменяя теперь из третьего соотношения Максвелла (смотри (III, 37))на , после простых преобразований получим:

(III, 39)

Для одного моля идеального газа 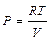. Подставляя это выражение в левую и правую части уравнения (III, 39)и считая объем постоянным, после дифференцирования будем иметь:

Полученный результат означает независимость внутренней энергии идеального газа от объема (и давления) при постоянной температуре. Это положение, принятое нами на основании опыта Гей‑Люссака — Джоуля (смотри стр.15), после приведенного вывода непосредственно вытекает из самого уравнения состояния идеального газа и законов термодинамики.

§ 5. Уравнение Гиббса‑Гельмгольца

Уравнение Гиббса-Гельмгольца позволяет определять изменение энергии Гиббса, сопровождающее химические реакции при любой заданной температуре, если известна зависимость теплоты химических реакций от температуры.

Для вывода уравнения запишем ещё раз формулу, определяющую энергию Гиббса (III, 18):

G = H – TS

Из уравнения (III, 23) и теоремы 1 (смотри стр.33) следует, что

, тогда можно записать

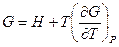
Полученное уравнение перепишем в следующем виде:

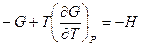
Разделим обе части полученного уравнения на Т²:

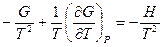
Нетрудно показать, что 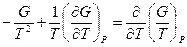. Опуская индекс и заменяя частную производную на полную, получим:

Для химической реакции это соотношение можно записать через изменение энергии Гиббса и энтальпии:

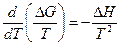, ( III, 40 )

где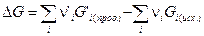

Выражение ( III,40 ) и являетсяизвестным уравнением Гиббса-Гельмгольца.

Оно лежит в основе аналитического вычисления зависимости D G от температуры.

Перед рассмотрением использования этого уравнения условимся применять его преимущественно к стандартным условиям, что может быть учтено, если D G и D H мы припишем соответствующие индексы:

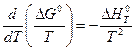( III, 41 )

Возьмем неопределенный интеграл соотношения ( III, 41 ):

,

где I — константа интегрирования, которая вычисляется для каждой конкретной реакции.

Чтобы вычислить интеграл в правой части полученного уравнения, подставим выражение для из формулы Кирхгофа (смотри (I, 74)):

( III, 42 )

Рассмотрим зависимость D C_P от температуры в двух приближениях:

1. Теплоемкости исходных веществ и продуктов различны, но их разность постоянна, т. е. D C_P = const. Интегрирование уравнения ( III, 42 ) дает:

2. При необходимости получения более точной зависимости D G от Т принимают во внимание, что теплоемкости участников реакции зависят от температуры и их представляют в виде эмпирических степенных рядов (смотри (I, 17)). Тогда интегрирование ( III, 42 ) с учетом(I, 75) дает:

. Константы данного уравнения D H ₀ и I определяются из вычисленных значени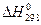й и химической реакции, которые, в свою очередь, могут быть найдены с использованием известных стандартных теплот образования и энтропий всех участвующих в химическом превращении веществ.

Анализ данных, полученных для различных процессов, показывает, что основная термодинамическая характеристика химической реакции , вообще говоря, довольно сильно зависит от температуры. Нередко при достижении определенной температуры знак меняется на противоположный, значит, при этом происходит изменение направления самой реакции.

Например, стандартная энергия Гиббса реакции

с повышением температуры изменяет знак с положительного на отрицательный при»1500 K. Следовательно, в стандартных условиях выше указанной температуры реакция получения ацетилена из природного газа становится самопроизвольной и ее практическое осуществление оказывается возможным.

Вернемся еще раз к определению энергии Гиббса (смотри (III, 18)):

G = H – TS

Применив это выражение к изотермическому процессу при постоянном давлении, можем записать:

D G_T = D H_T – T D S_T

Эта формула полезна тем, что она указывает на изменение энтропийного члена

T D S_T как на главную причину изменения D G реакции с температурой. Иначе говоря, энергия Гиббса реакции тем сильнее зависит от температуры, чем больше в ходе реакции изменяется энтропия системы.

Дата добавления: 2014-11-29