Статистическая интерпретация энтропии

В основу понятия энтропии как функции состояния положена макроскопическая концепция. Справедливость второго закона термодинамики связана с реальностью необратимых процессов. В отличие от необратимых макроскопических процессов, которые мы наблюдаем вокруг, законы классической и квантовой механики симметричны во времени, т. е. согласно законам механики система, которая может эволюционировать из состояния 1 в состояние 2, точно так же может эволюционировать из состояния 2 в состояние 1. Например, спонтанный поток молекул газа из одной части сосуда, где газ имеет бóльшую плотность, в другую часть сосуда, где газ имеет меньшую плотность, и обратный поток совершенно согласуются с законами механики. Но такой обратный поток противоречит второму закону термодинамики. Процессы, которые второе начало термодинамики отвергает как невозможные, не нарушают законов механики. В то же время все необратимые макроскопические процессы, такие, как теплообмен, происходят вследствие движения атомов и молекул, которое в свою очередь подчиняется законам механики; теплообмен обусловлен межмолекулярными столкновениями, при которых происходит передача энергии.

Каким образом необратимые процессы возникают из обратимого движения молекул?

Чтобы примирить обратимость механики с необратимостью термодинамики, М.Планк, основываясь на фундаментальных работах Л.Больцмана, предложил следующее соотношение между микроскопическими состояниями и энтропией:

S = k ln W (II, 34)

где W — число микросостояний, соответствующих тому макросостоянию, энтропия которого равна S (Величину W также принято называть термодинамической вероятностью. Подчеркнем, что термодинамическая вероятность отличается от математической вероятности, которая выражается числом, меньшим или равным единице.).

Постоянная k, введенная М.Планком, называется теперь постоянной Больцмана.

Следующий пример объясняет физический смысл W. Рассмотрим макросистему — некоторый ящик с газом. Пусть в одной части ящика находится N ₁ молекул этого газа, а в другой — N ₂ молекул. Каждая молекула газа может находиться как в одной, так и в другой части ящика. Общее число способов, которыми N ₁ + N ₂молекул можно распределить между частями ящика так, чтобы в одной части оказалось N ₁ молекул, а в другой N ₂ молекул, равно W. Число различных микросостояний с N ₁ молекулами в одной части ящика и N ₂ молекулами в другой составляет

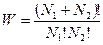
По Больцману, чем больше W, тем вероятнее, что это макросистема, т. е. система, которая подчиняется статистическим законам. Таким образом, необратимые процессы, происходящие с увеличением энтропии, соответствуют эволюции к наиболее вероятным состояниям. Равновесные состояния отличаются тем, что W в этих состояниях достигает максимума, т. е. они являются наиболее вероятными.

Можно показать, что в приведенном выше примере наиболее вероятным состоянием (W достигает максимального значения) является то, при котором N ₁ = N ₁.

ГЛАВА III.
ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА. ЭНЕРГИЯ ГИББСА. ПРИЛОЖЕНИЯ ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ

Дата добавления: 2014-11-29