Характеристические функции. Фундаментальные (канонические) уравнения состояния

Энергия Гиббса системы при постоянных давлении и температуре уменьшается при неравновесных (самопроизвольных) процессах, при равновесии её значение остаётся постоянным. Очевидно, равновесное состояние системы при данных P и Т соответствует минимуму энергии Гиббса.

Энергия Гиббса

Желая учесть в общей форме другие виды работы, кроме работы расширения, представим элементарную работу как сумму работы расширения и других видов работы:

d W = PdV + dW' (III, 15)

где dW ' — сумма элементарных работ всех видов, кроме работы расширения. Мы назовем эту величину элементарной полезной работой, а величину W' — полезной работой. Из уравнений (III, 11) и (III, 1) получаем:

d W' £ TdS – dU – PdV (III, 16)

Отсюда можно найти величину W ', получаемую при переходе системы из состояния 1 в состояние 2, интегрируя это уравнение в соответствующих пределах при постоянных температуре и давлении:

Сгруппировав все величины, относящиеся к одному состоянию, получим:

W' £ –(U ₂ – TS₂ + PV ₂) + (U ₁ – TS ₁+ PV ₁)(III, 17)

Обозначим через G выражения, стоящие в скобках правой части уравнения, которые являются функциями состояния, т. е.

G º U + PV – TS º H – TS (III, 18)

Тогда уравнение (III, 17) можно записать следующим образом:

W' £ – G₂ + G₁ = – (G ₂ – G ₁) = – DG (III, 19)

Так как D G не зависит от пути процесса, то, при условии постоянства P и Т, для равновесных процессов W' будет максимально:

W' _макс. = – G₂ + G₁ = – (G₂ – G₁) = – DG (III, 20)

где G — функция состояния, определяемая равенством (III, 18) и называемая энергией Гиббса. Таким образом, максимальная полезная работа при изобарно-изотермических процессах равна убыли энергии Гиббса.

Для получения полного дифференциала функции G при переменных P и Т дифференцируем уравнение (III, 18):

dG = dU – Т dS – SdT + PdV + VdP

Так как

dU £ TdS – PdV – d W',то

dG £ – SdT + VdP – d W ' (III, 21)

Из этого уравнения при постоянных Т и P получаем уравнение (III, 19) в дифференциальной форме.

При отсутствии всех видов работы, кроме работы расширения ( d W' = 0), в общем случае:

dG £ – SdT + VdP (III, 22)

а для равновесных процессов

dG = –SdT + VdP (III, 23)

Полагая T = const и P = const, а также при условии отсутствия всех видов работы, кроме работы расширения ( d W’ = 0 ), получаем из уравнения (III, 22):

(¶ G) _T,Р £ 0 (III, 24)

Так как любое самопроизвольное изменение термодинамической системы при постоянных давлении и температуре связано с уменьшением G, то прекращению всех процессов отвечает минимальное значение энергии Гиббса. Пользуясь произвольным масштабом, можно представить возможные и мыслимые изменения G в системе с помощью графика (рис. 7).

Рис. 7. Мыслимые изменения энергии Гиббса (G) в системе, сохраняющей постоянные давление и температуру. Равновесному состоянию соответствует минимум энергии Гиббса.

Ранее мы определили следующие термодинамические функции — свойства системы: внутреннюю энергию U, энтальпию H, энтропию S, энергию Гельмгольца F, энергию Гиббса G. Каждое из этих свойств можно представить в виде функции различных переменных, определяющих состояние системы. Однако в системах, состоящих из индивидуальных веществ, каждому из них можно приписать две переменные, которые можно считать «естественными» для той или иной функции.

В этом случае функция становится характеристической, т. к. через каждую из этих функций и ее производные в явном виде выражаются любые термодинамические свойства системы.

Термодинамическим свойством называется любое измеримое свойство макроскопической равновесной системы. Например, коэффициент объемного термического расширения или коэффициент изотермического сжатия — производные 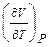и 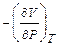, отнесенные к начальному объему системы. Эти величины измеряются в физических экспериментах.

Так, внутренняя энергия является характеристической функцией при переменных объеме V и энтропии S, т. е.

Если для равновесного процесса, когда в системе совершается только работа расширения, записать формулу объединенного первого и второго законов термодинамики (II, 19) относительно dU, то получим

dU = TdS – PdV ( III, 25 )

Принимая во внимание, что предложенное выражение является полным дифференциалом однозначной функции состояния U, мы можем записать:

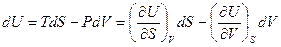
Из чего следует, что

и ( III, 26 )

Таким образом, производная внутренней энергии по энтропии при постоянном объеме равна температуре, а производная внутренней энергии по объему при постоянной энтропии равна давлению со знаком минус. При любых других переменных нельзя получить такие простые выражения свойств системы через производные внутренней энергии. Следовательно, для нее объем V и энтропия S являются естественными переменными. В свою очередь, внутренняя энергия при названных переменных — характеристическая функция.

Другими характеристическими функциями являются:

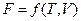
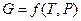
Запишем выражения для полных дифференциалов названных функций (смотри уравнения (I, 65), (II, 13), (III, 13), (III, 23)) и частных производных этих функций по их естественным переменным:

dH = TdS + VdP (III, 27)

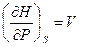( III, 28 )

dF = – SdT – PdV (III, 29)

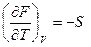
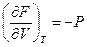( III, 30 )

dG = – SdT + VdP (III, 31)

( III, 32 )

Выражения (III, 25), (III, 27), (III, 29) и (III, 31) называются фундаментальными (каноническими) уравнениями состояния. Они образуют замкнутую группу, в которой две пары переменных — температура Т и энтропия S являются параметрами, связанными с теплотой. С другой стороны, давление Р и объем V связаны с работой.

Напомним, что каждая функция , , , 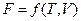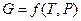или их производные, выражая в явном виде любое измеримое термодинамическое свойство, дают, таким образом, полную термодинамическую характеристику системы. Поэтому указанные функции называют характеристическими. Замена для данной функции естественных переменных на любые другие вполне возможна, но при этом лишает ее свойств характеристической функции.

Отметим также еще одно важное обстоятельство. Любая из этих функций может быть использована для того, чтобы сформулировать как критерий самопроизвольности процесса, так и критерий равновесия для систем, рассматриваемых при постоянстве естественных для этих функций переменных.

Для функций, имеющих размерность энергии (U,H,F и G), критерием самопроизвольности является их убыль, критерием равновесия — минимальное значение (этот вывод непосредственно следует из соотношений (II, 19), (III, 14) и (III, 24)).

Для энтропии (S), которую также можно рассматривать как характеристическую функцию переменных U и V или H и P, соответствующими критериями будут возрастание энтропии и её максимальное значение.

На протяжении веков было принято считать, что законы природы просты. Действительно, законы механики, гравитации, электромагнетизма допускают простые формулировки и могут быть точно представлены всего лишь несколькими уравнениями. Помимо простоты природа склонна также к «оптимизации», т. е. экономии. Явления природы часто происходят так, что некоторая физическая величина достигает своего минимального или максимального значения, или, если воспользоваться собирательным термином, достигает экстремального значения.

В равновесной термодинамике также реализуются принципы экстремумов. Приближение к равновесию происходит так, что термодинамические потенциалы достигают своего экстремального значения.

Дата добавления: 2014-11-29