Энергия Гиббса смеси идеальных газов. Определение химического потенциала

Энергия Гиббса является экстенсивной функцией, что позволяет рассчитать ее значение для смеси идеальных газов.

Представим себе резервуар, разделенный перегородками на секции, как показано на рис.8.

В каждую секцию помещают индивидуальный газ, причем все они имеют различную природу. Объем каждой секции равен V ₁, V ₂.. .V_i, объем всего резервуара равен V = V ₁ + V ₂ +... + V_i. Число молей каждого газа n ₁, n ₂.. .n_i. Во всех секциях газы имеют одинаковую температуру Т = const и одинаковое давление Р = const.

Рис. 8. Резервуар, разделенный на секции и заполненный газами разной природы
при Т = const и Р = const.

До перемешивания газов суммарная энергия Гиббса будет равна сумме энергий Гиббса всех газов, находящихся в отдельных секциях.

После удаления перегородок между секциями газы разной природы самопроизвольным образом перемешиваются вследствие процесса диффузии и все газы равномерно распределяются по объему резервуара V. Каждый газ в полученной смеси будет характеризоваться парциальным давлением P_i, причем P ₁ + P ₂ +... + P_i = P_общ..

Из определения энергии Гиббса (III, 18) следует:

G = U + PV – TS

Рассмотрим в этом выражении каждое слагаемое.

Согласно уравнению (I, 28) зависимость внутренней энергии 1 моль индивидуального i - ого вещества от температуры представляется следующим образом:

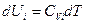(III, 43)

где C_Vi — молярная теплоёмкость при постоянном объёме i - ого газа. Так как для идеального газа теплоёмкость C_Vi не зависит от температуры, интегрируя при этом условии уравнение (III, 43) от нуля до Т, получим:

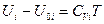или 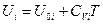(III, 44)

где U _{0 i} — внутренняя энергия 1 моль i - ого вещества при 0 К. Если в смеси этого вещества содержится n_i моль, то умножая обе части уравнения (III, 44) на n_i и суммируя по всем индивидуальным веществам системы, будем иметь:

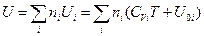(III, 45)

Второе слагаемое в выражении для энергии Гиббса, исходя из уравнения Менделеева — Клапейрона, запишем в виде:

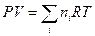(III, 46)

Рассмотрим третье слагаемое. Из уравнения (II, 23) для 1 моль идеального газа следует:

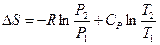
Положим 1 атм и T ₁ = 1 K, тогда

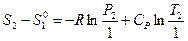или 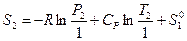(III, 47),

где 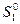— стандартная (так как относится к P ⁰ = 1 атм.) энтропия 1 моль идеального газа при 1 К, которая также называется энтропийной постоянной идеального газа. Индекс «2» теперь можно отбросить и выражение запишется в виде:

,

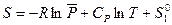где 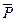— относительное давление. Стоящие под знаком логарифма величины 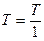и — безразмерные. Следует отметить, что величины P и P ⁰ могут быть выражены в любых, но обязательно одних и тех же единицах — атмосферах, паскалях, миллиметрах ртутного столба (торричелли) и т. д. Однако выражение давления в атмосферах имеет очевидное преимущество, т. к. в этом случае давление и относительное давление численно совпадают .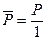

Таким образом, для 1 моля i - ого компонента газовой смеси мы можем записать:

(III, 48),

где 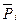— относительное парциальное давление i - ого компонента.

Умножив обе части выражения (III, 48) на n_i и суммируя по всем индивидуальным веществам в системе, получим:

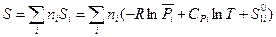(III, 49)

Подставив значения U, PV и S из уравнений (III, 45), (III, 46) и (III, 49) в выражение для энергии Гиббса, получаем следующий результат:

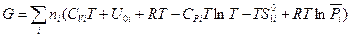(III, 50)

Первые пять слагаемых в этом уравнении зависят от природы индивидуального i ‑ ого вещества и температуры, но не зависят от состава смеси и давления. Алгебраическую сумму этих пяти слагаемых, стоящих в скобках, обозначим через 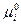. Тогда

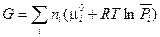(III, 51)

или, если ввести обозначение

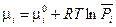(III, 52)

то выражение (III, 51) можно окончательно представить в таком виде:

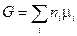(III, 53)

Величина 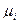называется химическим потенциалом i - ого вещества, а величина 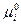— стандартным химическим потенциалом (при 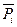=1) i - ого вещества.

Так как для идеальной газовой смес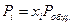и и 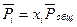, то уравнение

(III, 52) можно привести к виду:

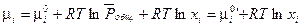(III, 54)

где 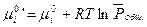(III, 55)

Если 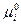есть функция только температуры, то 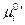зависит не только от температуры, но и давления.

Подставив значение m _i из уравнения (III, 54) в (III, 53), получим:

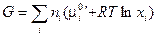(III, 56)

Для того, чтобы определить суммарную энергию Гиббса смеси идеальных газов, также следует принять во внимание изменение энергии Гиббса, обусловленное самим процессом смешения:

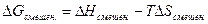
Оно может быть найдено, если принять во внимание, что для идеальных газов 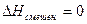. Ну, а изменение энтропии при смешении нами уже было определено ранее (смотри (II, 26)).

Таким образом,

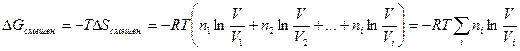
Так как при постоянстве температуры T = const произведение

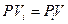= const, полученное уравнение можно переписать в следующем виде:

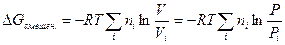
Принимая во внимание, что Р > 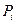и V > 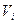, логарифм отношения этих величин — величина положительная, следовательно, 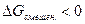, что полностью соответствует характеристике самопроизвольно протекающих процессов.

Итак, для энергии Гиббса смеси идеальных газов окончательно имеем:

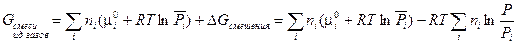
Дата добавления: 2014-11-29