
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование и обнаружение тенденции временного ряда
|
|
|
|
Наиболее распространенным способом моделирования тенденции временного ряда является сглаживание (аналитическое выравнивание) временного ряда – замена фактических уровней расчетными. Наибольшее распространение имеют линейные тренды:
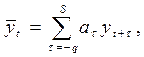
| (7.6) |
где 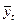 — выравненное значение уровня в момент t;
— выравненное значение уровня в момент t;
аτ — вес, приписываемый уровню ряда, находящемуся на расстоянии τ от момента t;
S — число уровней после момента t;
q — число уровней до момента t.
Процесс аналитического выравнивания состоит из двух этапов: выбора типа кривой и оценки параметров кривой.
Наиболее простым способом выбора типа кривой является построение графика эмпирических данных. По виду графика выбирается зависимость. Наиболее часто используются:
-полиномы:
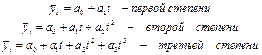
- различные экспоненты:
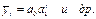
Для выбора типа кривой применяется также метод последовательных разностей, сущность которого заключается в нахождении первых, вторых и т.д. разностей уровней, т.е.
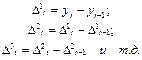
| (7.7) |
Расчет этих разностей ведется до тех пор, пока разности не будут приблизительно равными. Порядок этих разностей и принимается за порядок полинома.
По данным табл. 7.3 проверим наличие тенденции среднего уровня:
d=Ut-lt=14-0=14; при n=15; σ1=2,153; σ2=1,521 (приложение 2).
Задавшись уровнем значимости α=0,05 при n=14 (приложение 3), tкр(0,05;14)=2,14, тогда:

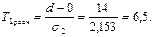
Таким образом, Т1расч> tкр(0,05;14)=6,5>2,14, т.е. гипотеза о наличии тенденции не отвергается.
Для выяснения формы полинома рассчитаем Δt.
Таблица 7.3
Энерговооруженность труда одного рабочего
(тыс.квт.час на 1 рабочего)
| Годы | Энерговооружен-ность, тыс. квт. ч. на 1 рабочего yt | Ut | l t | Δt1 | Δt2 |
| 0,81 | - | - | |||
| 0,85 | 0,04 | - | |||
| 0,90 | 0,05 | 0,01 | |||
| 0,94 | 0,04 | -0,01 | |||
| 0,98 | 0,04 | ||||
| 1,03 | 0,05 | 0,01 | |||
| 1,07 | 0,04 | -0,01 | |||
| 1,12 | 0,05 | 0,01 | |||
| 1,16 | 0,04 | -0,01 | |||
| 1,20 | 0,04 | ||||
| 1,26 | 0,06 | 0,02 | |||
| 1,31 | 0,05 | -0,01 | |||
| 1,35 | 0,04 | -0,01 | |||
| 1,33 | 0,04 | ||||
| 1,42 | 0,03 | -0,01 | |||
| SUt=14 | S l t=0 |
Так, например: 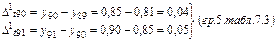
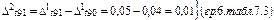
Из табл.7.3 видно, что первые разности Δt1 явно отличаются друг от друга, а средняя из вторых разностей очень мала (0,001), ею можно пренебречь. Следовательно, тенденция изучаемого ряда может быть описана полиномой первой степени:
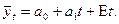
Для обнаружения тенденции временных рядов изучаются также изменения показателей за ряд периодов с помощью показателя среднего абсолютного прироста.
Величины абсолютных приростов ΔПр определяются как разность между последующими и предыдущими уровнями показателя:
ΔПр1=х1-х2; ΔПр2=х3-х2; ΔПр3=х4-х3; ΔПрn=xn-xn-1.
Число приростов всегда на единицу меньше числа уровней ряда.
 |
Средний абсолютный прирост динамического ряда за период определяется как средняя арифметическая:

| (7.8) |
Для составления прогноза с помощью абсолютного прироста исходный ряд преобразуется, получаем ряд у1, у2, у3 … уn, где у2= у1+ 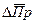 ; у3= у2+
; у3= у2+ 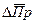 ; уn= уn-1+
; уn= уn-1+ 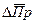 . Теоретически доказано, что данный ряд хорошо отображает тенденцию изменения уровней исходного ряда, если дисперсия исходного
. Теоретически доказано, что данный ряд хорошо отображает тенденцию изменения уровней исходного ряда, если дисперсия исходного
ряда относительно преобразованного меньше или равна половине среднего квадрата абсолютных приростов:
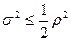
| (7.9) |
где
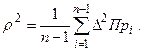
| (7.10) |
При выполнении данного условия считается, что с помощью преобразованного ряда уровни исходного ряда очищаются от случайной компоненты.
Зная закон изменения уровней ряда, можно построить прогноз на какое угодно число точек вперёд по формуле.
Например, имеются данные об уровне затрат на 1 грн. товарной продукции за двенадцать месяцев 2002 года. Необходимо с помощью среднего абсолютного прироста (табл.7.4) выявить тенденцию ряда.
Таблица 7.4
Расчет тенденции с помощью среднего абсолютного прироста
| Уровни, xi | ΔПрi=xi+1-xi | ΔПрi2=(xi+1-xi)2 | yn=yn-1+ 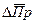
| ΔПр=(xi- 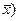
| (xi- 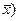 2 2
|
| 85,9 | 1,6 | 2,56 | 85,9 | -4,197 | 17,615 |
| 87,5 | -0,9 | 0,81 | 86,276 | -2,597 | 6,744 |
| 86,6 | 6,7 | 44,89 | 86,652 | -3,497 | 12,229 |
| 93,3 | -6,0 | 87,028 | 3,203 | 10,259 | |
| 87,3 | 7,1 | 50,41 | 87,404 | -2,797 | 7,823 |
| 94,4 | -0,7 | 0,49 | 87,78 | 4,303 | 18,516 |
| 93,7 | -3,03 | 9,1809 | 88,156 | 3,603 | 12,982 |
| 90,67 | 1,03 | 1,0609 | 88,532 | 0,573 | 0,328 |
| 91,7 | -0,52 | 0,2704 | 88,908 | 1,603 | 2,570 |
| 91,18 | -2,31 | 5,3361 | 89,284 | 1,083 | 1,173 |
| 88,87 | 1,17 | 1,3689 | 89,66 | -1,227 | 1,506 |
| 90,04 | - | - | 90,036 | -0,057 | 0,003 |
| Σxi=1081,16 | Σ ΔПрi=4,14 | ΣΔПрi2= 152,3772 | Σ(xi- 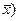 2 =91,748 2 =91,748
|
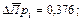
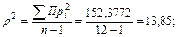
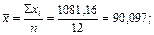
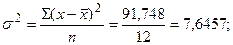
7,6457> 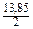
Следовательно, условие 7.9 не соблюдено, т.е. σ2>1/2ρ2, это означает, что плавной тенденции изменения показателя уровня затрат на 1 грн. товарной продукции обнаружить не удаётся, и данный метод для прогнозирования показателя не подходит.
Изучение изменений показателей за ряд периодов может проводиться с помощью скользящей средней.
С помощью скользящей средней прогнозируемые значения ряда можно вычислить, используя различные алгоритмы с учётом двух-трех и более точек предыстории:
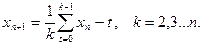 (7.11)
(7.11)
При k=n прогнозируемое значение ряда в момент времени tn+1 равно среднему арифметическому всех значений, при tn+1 – соответствующему среднему значению из (k) точек, непосредственно предшествующих прогнозируемой.
Построение скользящей средней первого порядка формализуется следующим образом:
1) выбирается длина первого периода;
2) определяется значение показателя за 1- й период;
3) рассчитывается средняя арифметическая показателя за 1-й период
(средняя первого порядка);
4) выбирается второй период таким образом, что первый месяц первого периода отбрасывается, а последующий добавляется;
5) определяется значение показателя за 2-ой период;
6) рассчитывается средняя арифметическая показателя за 2-й период;
7) выбирается 3-й период и т.д.
Построение скользящей средней второго порядка формализуется следующим образом:
1) рассчитывается сумма средних 1-го порядка первого и второго периода и т. д.;
2) рассчитывается средняя арифметическая второго и порядка.
Используя данные табл.7.5, рассчитаем скользящую среднюю.
Таблица 7.5
Расчет скользящей средней первого и второго порядков
| № периода | Периоды (5 месяцев) | Затраты на производство, тыс. грн. | |||
| За период | Средняя 1-го порядка | 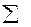 средних первого порядка средних первого порядка
| Средняя 2-го порядка | ||
| I-й | Январь-май | 440,6 | 88,12 | х | х |
| II-й | Февраль-июнь | 449,1 | 89,82 | 177,94 | 88,97 |
| III-й | Март-июль | 455,3 | 91,06 | 180,88 | 90,44 |
| IV-й | Апрель-август | 459,37 | 91,87 | 182,93 | 91,47 |
| V-й | Май-сентябрь | 463,77 | 92,75 | 184,62 | 92,31 |
| VI-й | Июнь-октябрь | 461,65 | 92,23 | 184,98 | 92,49 |
| VII-й | Июль-ноябрь | 456,12 | 91,22 | 183,45 | 91,73 |
| VIII-й | Август-декабрь | 452,46 | 90,49 | 181,71 | 90,86 |
Данные табл.7.5 показывают, что средняя первого порядка плавно возрастает до периода май-сентябрь, а затем с июня начинает снижаться, такая картина наблюдается и при рассмотрении значений средней второго порядка.
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 518; Нарушение авторских прав?; Мы поможем в написании вашей работы!