Адаптивные модели краткосрочного прогнозирования

Одним из направлений анализа является построение адаптивных моделей. Оценка параметров этой модели базируется на исходном временном ряде (фактических значениях показателя за определенный период времени), которые используются и для последующей корректировки показателей.

На основе новых данных, полученных на каждом шаге во времени (t), происходит дальнейшая корректировка (адаптация) параметров модели к новым условиям развития. Таким образом, модель постоянно обновляется на основании новой информации и приспосабливается к ней. Такие модели используются для прогнозирования изменения ежедневных остатков запасов на складах, изменения остатков денежных средств, частоты отказов оборудования, изменения курса акций и др.

Адаптивные модели дают более надежные результаты, чем регрессионные модели, которые «эксплуатируют» устаревшие, необновленные данные.

Простейшая адаптивная модель основывается на вычислении так называемой экспоненциальной средней.

Предположим, что исследуется временной ряд x_t. Экспоненциальное сглаживание – один из простейших приёмов выравнивания ряда. В его основе лежит расчет экспоненциальных средних.

При этом используется формула:

(7.12)

где S_t – значение экспоненциальной средней в момент времени t;

α – параметр сглаживания (α=const, 0<α<1);

β=1-α;

S_t-1 – предыдущее значение средней величины.

Выражение 7.12 можно представить в следующем виде (вместо β подставим ее значение):

(7.13)

где S_t-1 – прогноз средней на один шаг вперед;

x_t- S_t-1 – погрешность прогноза.

Экспоненциальная средняя на момент t здесь выражена как экспоненциальная средняя предшествующего периода (S_t-1) и доля (α) разницы текущего наблюдения (x_t) и экспоненциальной средней прогнозируемого периода.

Чем меньше α, тем меньше вариация (отклонения). В частности, если S_t-1 рассматривать как прогноз на шаг вперед, то величина x_t- S_t-1 есть погрешность этого прогноза, а новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит сущность адаптации.

Рассмотрим числовой пример сглаживания ряда курса акций.

Таблица 7.6

Расчет курса акций методом экспоненциального сглаживания

Дата	Курс акций, тыс.грн., xi	Курс акций (α=0,1) сглаж.	Дата	Курс акций, тыс.грн., xi	Курс акций (α=0,1) сглаж.	Дата	Курс акций, тыс.грн., xi	Курс акций (α=0,1) сглаж.
		506,4			502,4			509,9
		505,5			502,0			511,6
		505,3			502,0			512,8
		505,8			502,7			514,8
		505,8			505,0			515,8
		505,8			505,7			518,0
		505,2			506,1			520,1
		504,7			506,1			522,2
		504,3			507,0			524,3
		503,3			508,5			525,9

Определим S₀ как

Используя формулу 7.13, получим:

S₁=αx₁+(1-α)S₀=0,1*510+0,9*506=506,4 тыс.грн.

S₂=αx₂+(1-α)S₁=0,1*497+0,9*506,4=505,5 тыс.грн.

S₃=αx₃+(1-α)S₂=0,1*504+0,9*505,5=505,3 тыс.грн.. и т.д.

Рис.7.1. График динамики временного ряда и экспоненциальных средних

На рис.7.1. изображен график динамики временного ряда и экспоненциальных средних при α=0,1.

Обоснованным методом выявления тенденции является построение закона распределения. Наиболее простым в построении (так как имеет один параметр) является экспоненциальное распределение, которое используется в том случае, когда случайная величина «х» изменяется под воздействием случайных факторов (например, изменение стоимости курса акций, среднее время безотказной работы оборудования и др.)

Для того чтобы построить закон распределения, необходимо собрать исходную информацию о случайной величине, проверить достоверность исходной информации, построить группировку, построить гистограмму и принять гипотезу о возможном законе распределения, рассчитать параметры выбранного закона распределения, построить кривую распределения, по критерию согласия (Пирсона) проверить достоверность принятого закона распределения, сделать прогноз.

Плотность распределения экспоненциального закона распределения имеет вид:

(7.14)

где λ – интенсивность наступления события (является постоянной величиной, т.е. λ(х)= λ=const).Это значит, что среднее число величины х – величина постоянная:

Основными характеристиками экспоненциального распределения являются:

· вероятность наступления события х – Р(х);

· среднее значение случайной величины х – М(х);

· интенсивность наступления величины х – λ(х).

Вероятность наступления события определяется по формуле:

(7.15)

Рассмотрим пример. Курс акций банка в течение года изменялся в пределах от 0 до 4500 грн. Было продано 365 акций. Необходимо сделать прогноз стоимости одной акции на будущее.

Для построения гистограммы, кривой плотности, вероятности распределения и расчета параметра распределения составлена таблица 7.7.

Таблица 7.7

Исходные и расчетные данные о стоимости акций

Интервал курса акций, грн., xi	Количество акций, m	Середина интервала, xi	xm		()^2	()^2m
0-500
500-1000				-894
1000-1500				-394
1500-2000
2000-2500
2500-3000
3000-3500
3500-4000
4000-4500

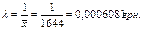
На рис.7.2 построена гистограмма курса акций. По характеру графика принимается гипотеза о распределении курса акций по экспоненциальному закону.

Проверка принятой гипотезы производится по критерию Пирсона по формуле:

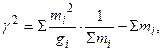
(7.16)

где m_i – частота интервала;

g_i – вероятность интервала (определяется как разность значений функции распределения в начале и конце интервала).

Для определения g_i необходимо определить g(х) -. вероятность конца интервала (g(500); g(1000) и т.д.) по формуле:

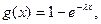
(7.17)

где е^-λх=Р(х) – вероятность наступления величины х.

Рис.7.2. Гистограмма курса акций

Таблица 7.8

Расчетные данные для определения вероятности наступления величины х

Середина интервала, х	λх	Р(х)=е^-λх		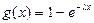λ е^-λх
	0,304	0,7378	0,2622	0,00049
	0,608	0,5444	0,4556	0,000331
	0,912	0,402	0,598	0,000244
	1,216	0,318	0,672	0,000193
	1,52	0,2187	0,7813	0,000130
	1,82	0,1620	0,838	0,0000985
	2,13	0,128	0,872	0,000079
	2,43	0,0889	0,911	0,000054
	2,74	0,0693	0,9307	0,0000042

После того, как определена вероятность конца интервала определяют вероятность каждого интервала g_i.

Таблица 7.9

Расчетные данные для определения вероятности интервала

Интервал	Количество акций, mi	mi^2	Вероятность интервала, gi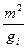
0-500			0,2662
500-1000			0,1934
1000-1500			0,1421
1500-2000			0,074
2000-2500			0,109
2500-3000			0,058
3000-3500			0,033
3500-4000			0,039
4000-4500			0,0693
Итого

Используя данные табл.7.9, определяем (c²):

c

Для определения вероятности согласия Р(c²) используем приложение 4. Определяем число степеней свободы:

k=e-r-1=9-1-1=7.

По приложению 4 при k=7 и c²=5,22 находим Р(c²)=0,66, что подтверждает достоверность принятой гипотезы о распределении курса акций.

ГЛАВА 8.

Дата добавления: 2014-12-10