Дисперсионный анализ

Вопрос о проверке существенности расхождения двух выбо­рочных характеристик может быть поставлен при срав­нении не только двух выборочных средних, но и двух выбо­рочных дисперсий. Для сравнения дисперсий применяется кри­терий, предложенный Рональдом Фишером, который называют дисперсионным отношением, или F-критерием.

Критерий Фишера представляет собой отношение двух дис­персий:

(8.35)

где и рассматриваются в качестве оценок одной и той же генеральной дисперсии.

При вычислении дисперсионного отношения в числителе бе­рется большая из оценок и , поэтому величина дисперсион­ного отношения может быть равна или больше единицы. Если F-критерий равен 1, то это указывает на равенство дисперсий, и во­прос об оценке существенности их расхождения снимается. Если же величина дисперсионного отношения больше единицы, то воз­никает необходимость оценить, случайно ли расхождение между дисперсиями. При этом очевидно, что чем больше величина дис­персионного отношения, тем значительнее расхождение между дисперсиями.

Для определения границ случайных колебаний отношения дисперсии Р.Фишером разработаны специальные таблицы F-pacпределения (см. Приложение VI). В этих таблицах указываются предельные значения F-критерия для различных комбинаций чис­ла степеней свободы числителя , и знаменателя , которые могут быть превзойдены с вероятностью 0,05 или 0,01. Число степе­ней свободы k, соответствующее большей дисперсии, определя­ет столбец таблицы, а число степеней свободы k₂,, соответствую­щее дисперсии , — строку таблицы.

Рассчитанная по фактическим данным величина дисперсион­ного отношения сопоставляется стабличной величиной дисперсионно­го отношения, соответствующей данному со­четанию числа степеней свободы числителя и знаменателя и при­нятому уровню значимости.

Гипотеза, которая проверяется с помощью этих таблиц, состо­ит в том, что сравниваемые дисперсии характеризуют вариацию признака в совокупностях, отобранных из одной и той же нор­мально распределенной генеральной совокупности или же ото­бранных из нормально распределенных генеральных совокупностей с одинаковой дисперсией.

Если фактическое дисперсионное отношение будет больше табличного, то лишь с вероятностью 0,05 или 0,01 можно утверж­дать, что различие между дисперсиями определяется случайны­ми факторами. Однако события, имеющие столь малую вероятность, считаются практически невозможными, а потому в этом случае с вероятностью 1 - α можно утверждать существенность раз­личий в величине дисперсий.

Если же фактическое значение дисперсионного отношения бу­дет меньше соответствующего табличного значения, например, при 1 %-ном уровне значимости, то с вероятностью 99% можно утверж­дать, что расхождение между дисперсиями несущественно.

Дисперсионный анализ приобретает самостоятельное значе­ние при оценке существенности расхождения нескольких средних, что позволяет проверить гипотезу о наличии связи между признаком, положенным в основу группировки, и результатив­ным признаком. В зависимости от количества факторов, определяющих вариацию результативного признака, дисперсионный анализ подразделяется на однофакторный и многофакторный. Методы дисперсионного анализа позволяют также проверить ги­потезу относительно формы корреляционной зависимости и оце­нить целесообразность включения в модель дополнительных фак­торов.

Рассмотрим применение дисперсионного анализа для случая однофакторного комплекса.

Пусть все n наблюдений разбиты на k групп в соответствии с определенным признаком и число наблюдений в j -й группе равно n_j Систему таких наблюдений в общем виде можно записать таким образом:

Номер группы Значения результативного признака

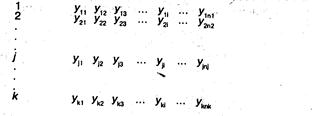
Обозначим общую среднюю для всей совокупности , а

сред­нюю — в соответствующей группе . Каждое индивидуальное от­клонение от общей средней складывается из двух частей: от­клонения от средней в соответствующей группе, т.е. величины 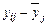, и отклонения в средней группе у от общей средней, т.е. 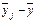, иначе Тогда сумма квадратов откло­нений всех наблюдаемых значений от общей средней будет равна:

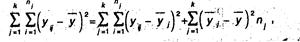(8.36)

где первое слагаемое в правой части представляет собой сумму квадратов отклонений наблюдаемых значений от групповых сред­них и характеризует вариацию внутри групп, а второе слагаемое — сумма квадратов отклонений групповых средних от общей сред­ней — характеризует вариацию между группами.

Колебания изучаемого признака внутри группы вокруг сред­ней возникают под влиянием прочих причин, исключая влияние фактора, положенного в основу группировки. Колеблемость груп­повых средних вокруг общей средней обусловлена влиянием при­знака-фактора. Если фактор, положенный в основу группиров­ки, не оказывает влияния на вариацию изучаемого признака, то дисперсия групповых средних будет отражать только влияние тех же самых прочих факторов, которые определяют и вариацию внут­ри групп, а потому отношение дисперсий будет близко к единице или отличаться от нее в силу наличия случайных колебаний. Пре­дельный размер этих колебаний можно установить по таблицам F-распределения (приложение 7).

При применении дисперсионного анализа для расчета диспер­сий учитывается число степеней свободы. В каждой группе при определении дисперсии мы располагаем 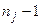степенями свободы, т.к. любое отклонение можем определить, зная 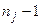отклонений и

Поскольку мы использовали k средних, а сумма , число степеней свободы для расчета внутригрупповой дисперсии равно 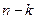. При расчете межгрупповой дисперсии мы рассматриваем k отклонений групповых средних от общей средней. Зная общую среднюю и k-1 групповых средних, можно определить любое из недостающих отклонений.

Тогда межгрупповая и внутригрупповая дисперсия с учетом числа степеней свободы будут соответственно равны:

(8.37)

(8.38)

Если группировочный признак оказывает влияние на вариа­цию результативного признака, то вариацию групповых средних нельзя считать обусловленной только случайными воздействия­ми, и это найдет отражение в различии величины межгрупповой и внутригрупповой дисперсии, т.е. F_расч. будет больше единицы. Если при этом F _расч. > F_табл., то с вероятностью 0,95 (0,99) можно утверждать, что между факторным и результативным признака­ми существует взаимосвязь.

Рассмотрим дисперсионный анализ на следующем примере.

За месяц известны данные о выработке рабочего за время ра­боты в первую и во вторую смены (см. табл. 8.13).

Таблица 8.13

Смена	Выработка рабочего, нормо-час
	12,1; 11,1; 12,6; 12,9; 11,6; 13,1; 12,6; 12,4; 11,6; 17,3; 12,9; 11,6; 12,4
II	9,9; 11,4; 13,4; 10,4; 12,9; 12,6; 13,9; 13,4; 12,4; 9.9

Можно ли считать, что расхождение между уровнями выработ­ки рабочего в первую и во вторую смены несущественно, т.е. мож­но ли считать, что генеральные средние в двух подгруппах одина­ковы и, следовательно, выработка рабочего может быть охаракте­ризована общей средней. Для того чтобы ответить на поставленный вопрос, рассчитаем среднюю выработку рабочих в каждой смене (см. графу 2 табл. 8.14). Величина средней выработки в первую и вторую смены различна. Теперь возникает вопрос о том, насколь­ко существенны эти расхождения, т.е. нужно проверить предполо­жение о возможном влиянии сменности на выработку рабочих. Используя данные графы 4 и графы 5, рассчитаем и .

Таблица 8. 14

Смена	Средняя выработка, нормо-часы	Число смен в месяце	Сумма квадратов отклонений вариантов от групповой средней	Квадраты отклонений групповых средних от общей средней
I	12,63		28,0877	0,0676
II	12,02		20,5960	0,1225
Итого			48,6837	-

Число степеней свободы для расчета внутригрупповой дис­персии равно 21(23-2), а для расчета межгрупповой дисперсии — 1(2-1).

Следовательно,.

В соответствии с числом степеней свободы числителя (1) и знаменателя (21) в таблице F-распределения для 5%-ного уровня значимости находим F_расч.= 4,32, а для 1%-ного уровня значимо­сти — F_табл.=8,02.

Так как F_расч. значительно меньше табличных значений, гипо­теза о несущественности различия выработки рабочего в первую и во вторую смены не опровергается, т.е. сменность не оказывает влияния на уровень выработки рабочего.

Дата добавления: 2014-12-10