Пример решения задачи №3

Запаздывающее звено.

Его динамическая характеристика представлена на рис.5,е. Это звено, в котором выходная величина воспроизводит без искажения входную величину, но с отставанием по времени т, называемого временем транспортного запаздывания,

передаточная функция -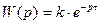

Частотные характеристики:

амплитудно-фазовая -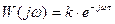

амплитудная -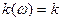

фазовая -

Примеры звена запаздывания: транспортеры, трубопроводы и др.

Задача №3

По заданной структурной формуле контактной схемы начертить соответствующую ей схему включения реле Р, и преобразовав её, найти эквивалентную упрощённую. Начертить схему, соответствующую упрощённой формуле. Структурную формулу для своего варианта взять из таблицы №5.

Таблица №5

Вариант	Структурная формула контактной схемы

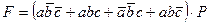
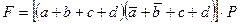
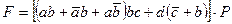
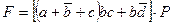
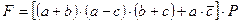
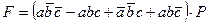
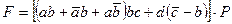
Задача 3 относится к разделу анализа и синтеза релейно-контактых схем. В основу аналитической формы записи релейных схем положены следующие обозначения:

А. В,... X, У... - воспринимающие, промежуточные и исполни­тельные элементы (обычно их рабочие обмотки);

а, b,... х, у,... -замыкающие контакты;

а, b,... х, у,... - размыкающие контакты;

а + b- параллельные соединения контактов;

а b - последовательное соединение контактов;

1 - постоянно замкнутая цепь;

0 - постоянно разомкнутая цепь;

f- структурная формула контактов;

F - структурная формула всей схемы.

При анализе и упрощении структурных формул однотактных ре­лейных устройств пользуются следствиями законов алгебры логики, основные из которых таковы:

При анализе и упрощении структурных формул однотактных релейных устройств пользуются следствиями законов алгебры логики, основные и которых таковы:

В дополнение к приведенным следствиям пользуются следую­щими теоремами.

Теорема 1. Если имеется схема соединения параллельно с замы­кающим контактом х, то все контакты х, имеющиеся в схеме, можно заменить нулями, а контакты х – единицами.

Если схема соединена параллельно с размыкающим контактом 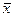, то все контакты 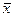, имеющиеся в схеме, можно заменить нулями, а кон­такты х – единицами.

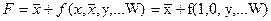
Пример 3.1. Упростить структурную формулу:

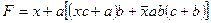
Решение 1. Применяем теорему:

Производим дальнейшие упрощения:

Так как , , 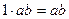то

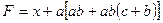
Вынесем общий множитель за скобки :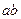

Но 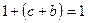, , 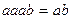поэтому:

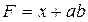
В результате упрощения получили схему, состоящую из трех контактов вместо одиннадцати.

Как видно, исходная схема имела «лишние» контакты и «лиш­ний» релейный элемент с, который не влиял на работу схемы. Вы­чертив схемы, соответствующие исходной и упрощенной структуре, легко убедиться, что исполнительный элемент F получит питания только при условии замыкания контакта х или одновременного за­мыкания контактов а и b.

Теорема 2. Если какая-нибудь схема включена последовательно с замыкающим контактом х, то все контакты х, имеющиеся в схеме, можно заменить единицами, а контакты 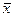- нулями.

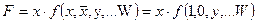
Если схема соединена последовательно с контактом 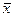, то все кон­такты 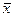, имеющиеся в схеме, можно заменить нулями, а контакты х – единицами/

Пример 3.2. Упростить структурную схему.

Решение. Применяем теорему 2.

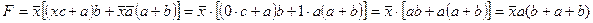
Таким образом, схема способна выполнять те же функции при наличии двух контактов.

Литература

1. Алехин С.А., Островская К.А. «Автоматизация и телемеханизация промыслов». М., Изд-во «Недра», 2006г.

2. Кузнецов В.А. «Основные вопросы надежности радиоэлектронной аппаратуры». М., Изд-во «Энергия», 2003г.

3. Базовский Н.Н. «Надежность. Теория и практика». М., Изд-во «Мир», 2001г.

4. Мамиконов А.Г., Гешелин М.Г. «Телемеханизация в нефтяной и газовой промышленности». М.,Изд-во «Недра», 1999г.

5. Погонин В.А., Елизаров И.А., Третьяков А.А., Назаров В.Н., Скворцов С.А. «Автоматизация технологических процессов и производств». Изд-во: Москва, 2008г.

6. Ершов М.С., Яризов А.Д. «Электрооборудование и станции управления технологических установок механизированной добычи нефти». Изд-во: Москва. Учебное пособие 2008г.

7. Андреев Е.Б., Ключников А.И., Кротов А.В., Попадько В.Е., Шарова И.Я. « Автоматизация технологических процессов добычи и подготовки нефти и газа». Изд-во: Москва., Учебное пособие 2008г.

8. Ильин В. А. «Системы телемеханики для рассредоточенных объектов». Библиотека по автоматике, выпуск 015. Издательство: Госэнергоиздат., 2011г.

9. Мовсудзе А.Э., Сощенко А.Е.; «Телемеханизация и автоматизация в нефтяной и газовой промышленности» - М.: Изд.центр. Недра,2008г.

10. Ильин В. А. «Большие системы телемеханики». Библиотека по автоматике, вып. 227. Издательство: Энергия, 2010г.

11. Карпов Ю. Г. «Теория автоматов». СПб.: Питер, 2002г.

Дата добавления: 2014-12-10