
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Восстановление оригинала
|
|
|
|
Для использования операционного исчисления при решении
задач нужно не только уметь находить изображение оригинала, но и по изображению восстанавливать соответствующий ему оригинал. Для этого полезны следующие таблицы.
Таблица 1
ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
| Оригинал | Изображение |

| 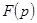
|

| 
|

| 
|
 , , 
| 
|

| 
|

| 
|
Окончание табл. 1

| 
|

| 
|

| 
|
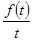
| 
|
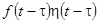 , , 
| 
|

| 
|
 , , 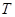 – период – период
| 
|
Таблица 2
ПРОСТЕЙШИЕ ОРИГИНАЛЫ И ИЗОБРАЖЕНИЯ
| Оригинал | Изображение | Оригинал | Изображение |

| 
|

| 
|
 , , 
| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
| Окончание табл. 2 | |||

| 
| 
| 
|

| 
|

| 
|

| 
| 
| 
|

| 
| 
|

|
Здесь приведены наиболее часто встречающиеся в задачах простейшие оригиналы и их изображения. Некоторые из них были получены ранее и выделены в рамках. Остальные рассмотрены ниже в примерах.
ПРИМЕР 20. Найти оригинал для изображения  .
.
Решение. Разложим 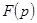 на простейшие дроби:
на простейшие дроби:  . Коэффициенты
. Коэффициенты 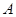 и
и  находим по методу неопределенных коэффициентов:
находим по методу неопределенных коэффициентов:  ,
,  , следовательно,
, следовательно,
 .
.
Итак, имеем соотношение  .
.
Аналогично устанавливаются формулы
 ,
,
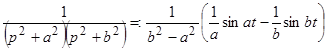 .
.
ПРИМЕР 21. Найти оригинал для изображения  .
.
Решение. Имеем  (см. пример 7). Интегрируя оригинал (см. табл. 1), получаем
(см. пример 7). Интегрируя оригинал (см. табл. 1), получаем
 .
.
Рассмотрим несколько примеров нахождения изображений и восстановления оригиналов с помощью табл. 1 и 2.
ПРИМЕР 22. Найти оригинал  , если его изображение есть
, если его изображение есть  .
.
Решение. Изображение разложим на простейшие дроби:  . Но
. Но  ,
,  . Окончательно имеем
. Окончательно имеем  .
.
ПРИМЕР 23. Пусть 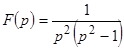 . Найти
. Найти  .
.
Решение.  .
.
Пользуясь таблицей, находим  ,
,  , следовательно,
, следовательно,  .
.
ПРИМЕР 24. Пусть  . Найти
. Найти  .
.
Решение. Преобразуем заданное изображение:
 .
.
Воспользуемся свойством интегрирования оригинала: по таблице находим  , тогда
, тогда  .
.
Из табл. 2 находим  , или
, или  . Следовательно, искомый оригинал
. Следовательно, искомый оригинал  .
.
ПРИМЕР 25. Восстановить оригинал по изображению:
а)  ; б)
; б)  .
.
Решение. а) по табл. 2 находим  и
и  .
.
По табл. 1 учитываем запаздывание аргумента оригинала, а именно 
 и
и
 . Окончательно получаем оригинал
. Окончательно получаем оригинал  , или
, или

б) аналогично имеем последовательно  ,
,  .
.
ПРИМЕР 26. Найти оригинал  по его изображению
по его изображению  .
.
Решение. Сначала пытаемся найти оригинал сразу по табл. 2, но в данном примере это не удается. Поэтому сведем 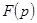 к табличным выражениям, преобразуя следующим образом:
к табличным выражениям, преобразуя следующим образом:
 .
.
По табл. 2 находим  и
и  или
или  .
.
Окончательно оригинал запишется так:
 .
.
Таким образом, для отыскания оригинала по известному
изображению иногда можно представить изображение в виде суммы табличных изображений, затем найти оригинал каждого слагаемого, а результаты сложить. Обращение преобразования Лапласа в общем виде рассмотрено далее.
Задание. Восстановить оригинал  по изображению:
по изображению:
а)  ; б)
; б)  .
.
Ответы: а)  ;
;
б)  .
.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3116; Нарушение авторских прав?; Мы поможем в написании вашей работы!