Формулы Дюамеля. Применение их к решению дифференциальных уравнений

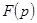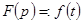Иногда изображения приводятся к виду , причем оригиналы изображений и известны, т.е. и . Тогда оригинал изображения можно найти через оригиналы и следующим образом.

Выражение можно записать в виде

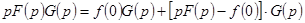или

.

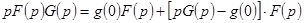По свойству дифференцирования оригинала имеем и Применяя теперь теорему Бореля к изображениям и , получаем

или

. (23)

Аналогично получается формула

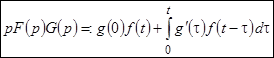. (24)

Соотношения (23) и (24) называются формулами Дюамеля, а интегралы в правых частях формул называются интегралами
Дюамеля. Заметим, что можно использовать свойство симметрии свертки функций и , а также 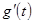и , и получить еще две формулы Дюамеля:

. (25)

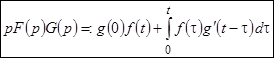. (26)

Формулы Дюамеля применяются, например, для решения
дифференциальных уравнений в некоторых ситуациях.

Пусть известно решение 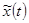линейного дифференциального уравнения с постоянными коэффициентами с единичной правой
частью и нулевыми начальными условиями в нуле:

, (27)

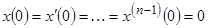. (28)

Найти решение аналогичного дифференциального уравнения с правой частью :

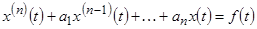(29)

при тех же начальных условиях (28).

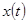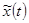Решение задачи. Предположим, что искомое решение , функция и решение уравнений (27) – (28) являются оригиналами, причем 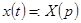, , 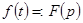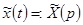. Тогда для дифференциальных уравнений (27) – (28) и (29) – (28) операторные уравнения запишутся соответственно

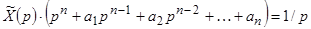и

.

Разделив равенства, получим 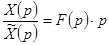или 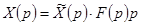. Применяя к 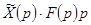формулы Дюамеля (23) – (26), получим решение уравнения (29) при (28), например, в виде или и т.д.

ПРИМЕР 35. Найти решение дифференциального уравнения при .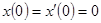

Решение. Рассмотрим вспомогательное уравнение 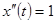при 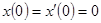. Ему соответствует решение , .

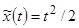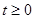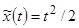Для решения исходного уравнения воспользуемся формулой Дюамеля (24) при и , получаем

.

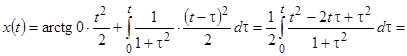
Итак, решение уравнения есть

.

Теорема Бореля и формулы Дюамеля дают дополнительные возможности нахождения оригинала по изображению.

Задание

1. Используя формулу Дюамеля, решить дифференциальное уравнение при .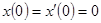

Ответ: , .

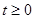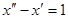2. Проверить, что – решение дифференциального уравнения при 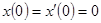. Найти решение
уравнения при .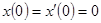

Ответ: , .

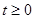* Пьер Симон Лаплас (1749 – 1827) – французский астроном, математик

* Оливер Хевисайд (1850 – 1925) – английский физик

* Эмиль Борель (1871 – 1956) – французский математик

Дата добавления: 2014-12-16