
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И изображения
|
|
|
|
ТЕОРЕМЫ О СДВИГЕ АРГУМЕНТОВ ОРИГИНАЛА
Теорема (о запаздывании оригинала)
Если  и
и 
 , то для
, то для 
справедливо соотношение
 . (13)
. (13)
 Иначе говоря, если процесс, описываемый оригиналом
Иначе говоря, если процесс, описываемый оригиналом 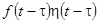 , запаздывает на
, запаздывает на  по сравнению с первоначальным
по сравнению с первоначальным  (см. рисунок), то изображение, соответствующее этому процессу, получается умножением изображения первоначального оригинала на
(см. рисунок), то изображение, соответствующее этому процессу, получается умножением изображения первоначального оригинала на 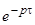 . В самом деле, для оригинала
. В самом деле, для оригинала 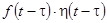 по определению (1) изображение
по определению (1) изображение
запишется в виде

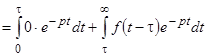 , поскольку
, поскольку  для каждого
для каждого 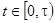 . Проведем замену переменной
. Проведем замену переменной  ,
, 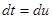 . Тогда
. Тогда
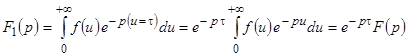 .
.
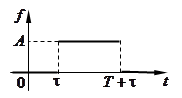
ПРИМЕР 13. Найти изображение прямоугольного импульса амплитуды 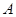
продолжительностью 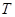 с запаздыванием
с запаздыванием  (см. рисунок).
(см. рисунок).
Решение. Импульс

можно записать аналитически с помощью единичной функции в виде

Используя свойства преобразования Лапласа и теорему о
запаздывании оригинала, получаем
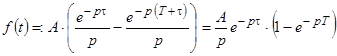 .
.
Замечания: 1. При использовании теоремы запаздывания
оригинала рекомендуется всегда оригинал записывать с множителем 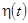 . В противном случае возможны ошибки. Например, для оригинала
. В противном случае возможны ошибки. Например, для оригинала 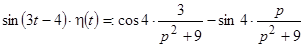 , а для оригинала
, а для оригинала  .
.
2. Теорема запаздывания оригинала используется для нахождения изображения кусочно-непрерывных функций (иногда их называют "склеенными" функциями).
ПРИМЕР 14. Найти изображение оригинала
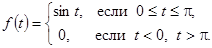
Решение. Можно записать 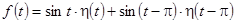 . Тогда
. Тогда 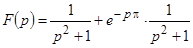 .
.
Здесь имеем 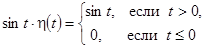 и
и
 Суммируя эти функции на промежутках
Суммируя эти функции на промежутках  ,
,  ,
,  ,
,
получаем значение функции  .
.
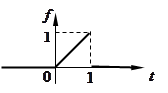 ПРИМЕР 15. Найти изображение функции, представленной графиком на рисунке.
ПРИМЕР 15. Найти изображение функции, представленной графиком на рисунке.
Решение. Функция
 может быть представлена через единичную функцию
может быть представлена через единичную функцию 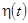 , а именно
, а именно  . Для того, чтобы применить теорему о запаздывании оригинала, преобразуем второе слагаемое к виду
. Для того, чтобы применить теорему о запаздывании оригинала, преобразуем второе слагаемое к виду  . Окончательно получаем
. Окончательно получаем  и по формуле (13)
и по формуле (13)  .
.
ПРИМЕР 16. Найти изображение функции, представленной графиком.
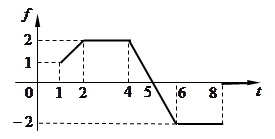 Решение. По рисунку имеем
Решение. По рисунку имеем
 Через единичную функцию
Через единичную функцию 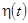 запишем
запишем  так, чтобы на каждом из промежутков значение
так, чтобы на каждом из промежутков значение  совпало с вышеуказанным, а в точках "стыка" графика "вводилась" единичная функция с соответствующим сдвигом аргумента. Получаем
совпало с вышеуказанным, а в точках "стыка" графика "вводилась" единичная функция с соответствующим сдвигом аргумента. Получаем
 и соответственно
и соответственно
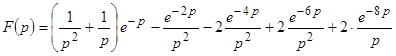 .
.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 4702; Нарушение авторских прав?; Мы поможем в написании вашей работы!