
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференцирование оригинала
|
|
|
|
Если 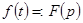 , а функции
, а функции 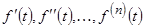 – оригиналы, то справедливы соотношения
– оригиналы, то справедливы соотношения
то 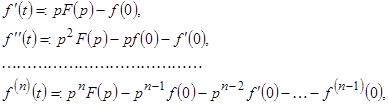 (7)
(7)
где 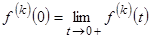 ,
, 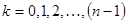 .
.
В самом деле, из формулы (1) после интегрирования по частям получаем 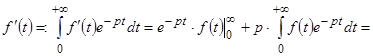
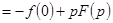 , т.е.
, т.е. 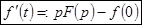 .
.
Здесь, как и ранее предполагалось, 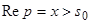 , и поэтому имеем
, и поэтому имеем 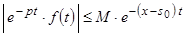 , т.е.
, т.е. 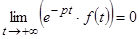 .
.
Применяя полученную формулу к функции 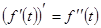 ,
,
получаем соотношение
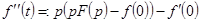 или
или 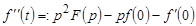 .
.
Методом математической индукции устанавливается справедливость соотношений (7) при каждом значении 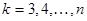 .
.
Формулы (7) становятся более простыми при  для
для 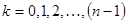 . В этом случае имеем
. В этом случае имеем
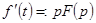 ,
, 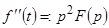 ,
, 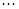 ,
, 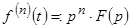 ,
,
т.е. видим, что дифференцирование оригинала  сводится к
сводится к
умножению на 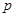 изображения
изображения 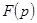 .
.
Изображения функций и их производных используются при
решении линейных дифференциальных уравнений с постоянными коэффициентами вида 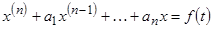 (8)
(8)
с начальными условиями 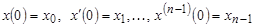 ,(9)
,(9)
здесь 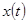 – искомое решение;
– искомое решение; 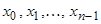 – заданные числа.
– заданные числа.
Предположим, что искомое решение этой задачи Коши дифференциального уравнения 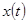 и его производные
и его производные 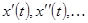 ,
, 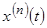 , а также функция
, а также функция  являются оригиналами. Тогда,
являются оригиналами. Тогда,
используя свойства изображений, можно перейти от дифференциального уравнения (8) с начальными условиями (9) к операторному уравнению
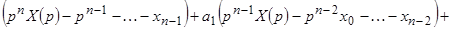
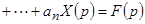 , где
, где 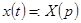 ,
, 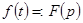 .
.
Это уравнение является линейным алгебраическим уравнением
относительно 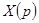 . Разрешив его, найдем
. Разрешив его, найдем 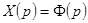 – изображение искомого решения
– изображение искомого решения 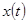 . Далее по
. Далее по 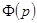 восстанавливаем оригинал
восстанавливаем оригинал 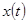 – требуемое решение задачи Коши (8) – (9).
– требуемое решение задачи Коши (8) – (9).
ПРИМЕР 8. Найти решение дифференциального уравнения 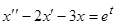 при
при 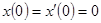 .
.
Решение. Переходим к операторному уравнению: полагаем 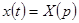 , находим
, находим 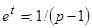 и записываем
и записываем 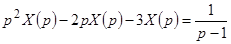 . Из этого уравнения получаем
. Из этого уравнения получаем 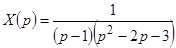 или
или 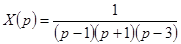 .
.
Для восстановления 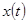 по его изображению
по его изображению 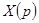 можно разложить
можно разложить 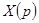 на простейшие дроби
на простейшие дроби
 .
.
Коэффициенты разложения 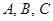 найдем методом неопределенных коэффициентов, приводя дроби в правой части к общему знаменателю и приравнивая числители. При любых
найдем методом неопределенных коэффициентов, приводя дроби в правой части к общему знаменателю и приравнивая числители. При любых 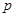 имеем
имеем 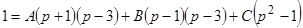 , в том числе
, в том числе
при 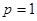 получаем
получаем 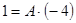 или
или 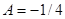 ;
;
при 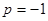
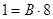 или
или 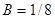 ; при
; при 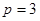
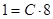 или
или 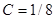 .
.
Окончательно имеем 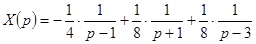 .
.
Используя свойства изображения и пример 6, получаем
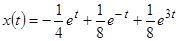 ,
, 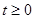 .
.
Непосредственной подстановкой 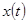 в заданное уравнение можно убедиться в правильности полученного решения.
в заданное уравнение можно убедиться в правильности полученного решения.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1568; Нарушение авторских прав?; Мы поможем в написании вашей работы!