Интегрирование оригинала

Если – оригинал и 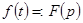, , 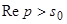то функция 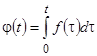также является оригиналом, причем

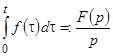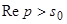, , (10)

т.е. интегрированию оригинала соответствует деление изображения на .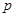

В самом деле, функция 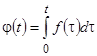удовлетворяет определению оригинала:

1) по свойству определенного интеграла с переменным пределом функция 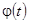либо непрерывна всюду, либо имеет конечное число точек разрыва первого рода на произвольном отрезке конечной
длины;

2) 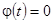при 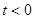, так как 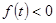при 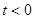, причем ;

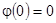3) для

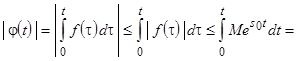
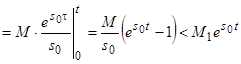, здесь использованы свойства оригинала , 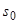– показатель роста функций и .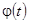

Обозначим изображение функции 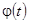через 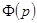. По свойству интеграла с переменным верхним пределом 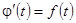и (см. формулу (7)). Из равенства 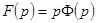устанавливаем (10).

ПРИМЕР 9. Применить формулу (10) к степенным функциям , .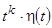

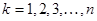Решение. Представим , получим соотношение 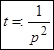, аналогично 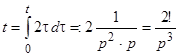, т.е. .
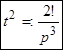В общем случае .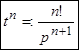

Дата добавления: 2014-12-16