Оригинал. Изображение

XXII. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

В основе операционного исчисления лежит преобразование
Лапласа*. Множество функций-оригиналов отображается в множестве функций-изображений, при этом операции над оригиналами переходят в некоторые операции над изображениями. В частности, операции дифференцирования и интегрирования оригиналов переходят в действия соответственно умножения и деления во множестве
изображений. Поэтому линейное дифференциальное уравнение
в множестве оригиналов преобразуется в алгебраическое уравнение
в множестве изображений. Решив полученное алгебраическое уравнение, находим прообраз его решения в множестве оригиналов,
затем восстанавливаем решение исходного дифференциального уравнения.

Такова основная идея применений операционного вычисления как символического метода решения некоторых дифференциальных уравнений и систем дифференциальных уравнений.

В настоящее время операционное исчисление широко используется для решения многих прикладных задач, в частности задач
радиотехники и электротехники.

Оригиналом или начальной функцией называется функция действительного переменного , удовлетворяющая следующим условиям:

1) ;

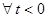
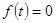2) при 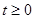функция имеет на каждом отрезке конечной длины пустое или конечное множество точек разрыва первого рода;

3) при 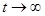функция 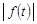возрастает не быстрее показательной функции, т.е. 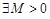, 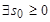такие, что выполняется
неравенство 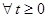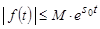, обычно под числом –
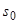показателем роста функции – понимается наименьшее из
возможных чисел.

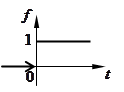ПРИМЕР 1. Единичная функция Хевисайда* обозначается через 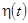и записывается в виде 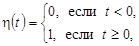график ее представлен на рисунке. Функция 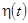является оригиналом, причем , .

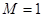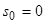Очевидно, что для произвольной функции 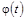, определенной на 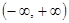и удовлетворяющей условиям 2 и 3, произведение 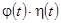является оригиналом (например, 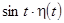, 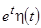и т.д.)

ПРИМЕР 2. Функция является оригиналом, причем для всех имеем 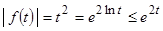, т.е. , .

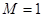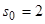ПРИМЕР 3. Функция 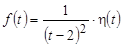не является оригиналом, поскольку в точке 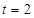функция имеет разрыв второго рода.

ПРИМЕР 4. Функция 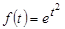не является оригиналом, так как при растет быстрее любой показательной функции вида .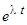

Нетрудно проверить, что произведение оригинала на число, сумма и произведение конечного множества оригиналов есть также оригинал.

Изображением (по Лапласу) оригинала 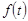называется
комплекснозначная функция 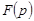комплексной переменной 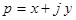(иногда 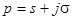), определяемая интегралом Лапласа:

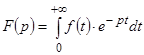. (1)

Здесь интегрирование проводится по действительной переменной , , 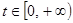т.е. интеграл (1) является несобственным, зависящим от параметра 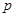, причем область определения функции 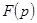является совокупностью тех комплексных чисел 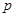, для которых интеграл (1) имеет смысл.

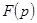Переход от оригинала к изображению по формуле (1) есть преобразование Лапласа (сокр. ПЛ); будем обозначать его так:

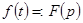
(читается: "оригиналу соответствует изображение ").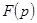

Дата добавления: 2014-12-16