Теорема 2 (о рациональном изображении)

Теорема 1

Пусть изображение 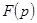аналитически продолжимо на полуплоскость , причем продолженная функция удовлетворяет
условиям:

1) 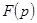при имеет конечное число изолированных
особых точек ;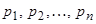

2) при стремится к нулю равномерно относительно .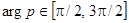

Тогда интеграл (17) вычисляется по формуле

. (18)

Пусть изображение 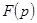есть правильная несократимая рациональная дробь 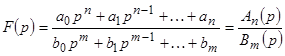, . Пусть знаменатель имеет корни 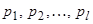кратности соответственно так, что , .

Тогда оригинал может быть найден по формуле

. (19)

Частный случай теоремы (о рациональном изображении) для ситуации, когда все корни знаменателя являются простыми, т.е. , , позволяет находить
оригинал по формуле

. (20)

ПРИМЕР 27. Найти оригинал , соответствующий изображению .

Решение. Знаменатель имеет корни кратност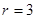и и 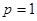кратности . Находим вычеты функции в полюсах и , а именно

.

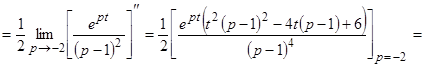
Аналогично

.

Окончательно искомый оригинал запишется в виде

, .

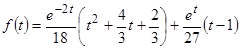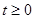ПРИМЕР 28. Найти оригинал , если изображение его есть .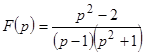

Решение. Знаменатель имеет только простые нули , 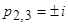. Поэтому

.

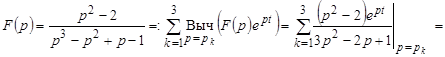
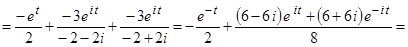
Итак, , .

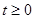22.7. ПРИМЕРЫ ПРИМЕНЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ

ПРИМЕР 29. Найти частное решение уравнения

,

удовлетворяющее начальным условиям .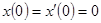

Решение. Обозначим изображение искомого решения 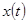через 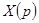, т.е. 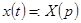, тогда .

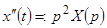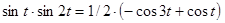Правую часть уравнения представим в виде , поэтому изображение ее есть .

От дифференциального уравнения переходим к операторному

,

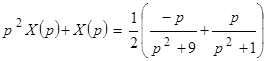откуда

, .

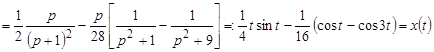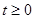Рекомендуем всегда проводить проверку найденного решения, т.е. убедиться, что найденная функция удовлетворяет дифференциальному уравнению и указанным в задаче начальным условиям.

ПРИМЕР 30. Найдите решение системы дифференциальных уравнений удовлетворяющее начальным условиям , , .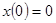

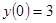Решение. Обозначим 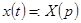, , 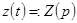. Тогда , , .

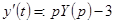Каждое из дифференциальных уравнений системы заменим операторным уравнением:

Полученную систему линейных алгебраических уравнений
решаем методом Крамера:

, и или .

Аналогично

;

.

Ответ: ; ;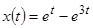

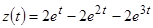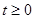, . Рекомендуем провести проверку полученного результата.

В курсах теоретических основ электроники и радиотехники часто решаются линейные неоднородные дифференциальные уравнения, правая часть которых – "склеенная" функция.

Рассмотрим пример решения уравнения подобного типа.

ПРИМЕР 31. Найти решение уравнения

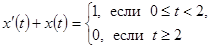при .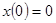

Решение. Пусть 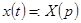, тогда и левая часть уравнения имеет изображение . Чтобы найти изображение правой части уравнения, запишем через единичную функцию Хевисайда: .

По теореме запаздывания имеем .

Итак, данное дифференциальное уравнение переходит в операторное уравнение 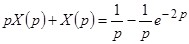, решение которого

.

Находим оригиналы слагаемых:

; .

Поэтому имеем 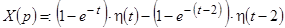или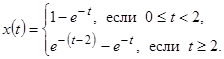

Задания

1. Решить уравнение

при .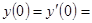

Ответ: .

2. Решить систему уравнений при 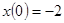, . Ответ:

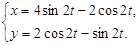
2. 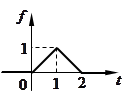Решить дифференциальное уравнение при 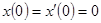, где функция задана графиком как треугольный импульс (см. рисунок).

Ответ: если 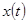– решение и ,

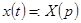, то . Имеем

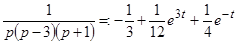и

.

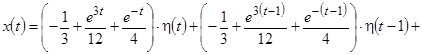
22.8. СВЕРТКА ОДНОСТОРОННИХ ФУНКЦИЙ; ЕЕ СВОЙСТВА. ТЕОРЕМА БОРЕЛЯ^*

Сверткой функций и , заданных на 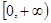, называется функция, равная интегралу , ;
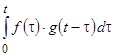она обозначается , т.е.

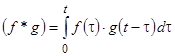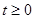, . (21)

Свойства свертки

1. Симметрия, т.е. .

В самом деле, изменяя порядок интегрирования и полагая , получаем равенство

.

2. Если и – оригиналы, то и их свертка также является оригиналом с показателем роста, равным наибольшему из показателей роста функций и . Рекомендуем доказать самостоятельно это утверждение или же посмотреть в [3].

ПРИМЕР 32. Найти свертку функций и .

Решение. 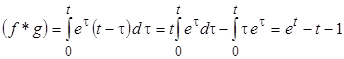, здесь ко второму интегралу применено интегрирование
по частям.

Дата добавления: 2014-12-16