Немесе комбинаторика 2 страница

29. Кубтың 6 жағын 6 реңмен бояған. Кубты айналдырғанда қабаттасатын боялуды бірдей деп есептесе неше әр түрлі жағдаймен бояуға болады? Жауабы: 6!/24

30. n нүктенің дәл m нүктесі бір түзудің бойында, басқа қандай да үшеуі бір түзудің бойында жатпайтын болса а) Осы нүктелерді бастырып неше түзу жүргізуге болады?

Нұсқау жауап: 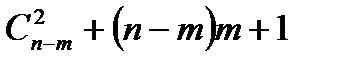б) Осы нүктелерде төбелері болатын неше үшбұрыш сызуға болады?

31. Дөңес n бұрыштың диагоналдарының қиылысу нүктелері ең көп дегенде нешеу болады?

Нұсқау жауап: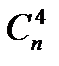

32. Бір түзудің бойында 8 нүкте, оған параллель келесі түзудің бойында 11 нүкте берілген. Осы нүктелерде төбелері болатын

а) Үшбұрыш нешеу?

б) Төртбұрыш нешеу?

в) Тармақтары берілген түзулерде жатпайтын өзін өзі қимайтын 16 төбесі болатын қисық сызық нешеу?

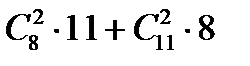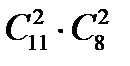Нұсқау жауап: а) , б) , в)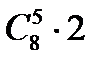

33. а) 15 түзу, б) 4 шеңбер жазықтықты ең көп дегенде неше бөлікке бөледі?

Жауабы: а) 121, б) 14

34. О нүктесінен n сәуле жүргізілген. Осы сәулелер қабырғалары болатын неше бұрыш болады?

35. Дөңес 7 бұрыштың төбелерінде төбесі болатын, ал 7 бұрыштың қабырғалары қабырғасы болмайтын үшбұрыштардың санын тап.

Нұсқау жауап: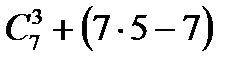

36. а) 6∙6 өлшемді шахмат тақтасының сол жақ төменгі бұрышындағы король оңға, не жоғары, немесе оң-жоғары бағытында диагонал бойымен көшу арқылы оң жақ жоғарғы бұрыштағы көзге неше тәсілмен бара алады?

б) 7∙7 өлшемді тақтада тақтаның центріндегі көзді басып өтпейтін жағдайда бұл есепті шеш.

Нұсқау: Тақтаның оң және астыңғы шетіндегі әр көзге бір көзден, ал басқа барлық көзге үш көзден келе алатынына көз жеткізіп, заңдылықты тап.

37. 1∙8 шахмат тақтасының сол жақ шеткі көзіндегі арба оң жақ шеткі нүктеге а) әр түрлі неше маршрутпен жете алады?

б) Солдан санағанда 5-көзге түспейтін

в) 5-көзге қайткен күнде түсетін маршруттар нешеу?

г) Арба 1 не 2 аттап көшетін жағдайда а) - в) есептерді шеш.

38. Цифр қайталанбай жазылған 5 таңбалы жұп сан нешеу?

Нұсқау: Соңғы цифры 0 болатын және 0- ден өзгеше жұп цифрлар болатын жағдайларды жеке жеке қарастыр.

Жауап: 9·8·7·6·1+8·8·7·6·4

39. 7 алма, 4 мандарин, 9 алмұрттан неше әр түрлі тәсілмен жеміс таңдауға болады?

Нұсқау жауап: (7+1)(4+1)(9+1) -1.

40. 0; 4; 6; 8 цифрлары кірмейтін 4-ке бөлінетін 5 таңбалы сан нешеу? Жауабы: 5·6³

41. Қатар 2 цифры әр түрлі 5 таңбалы сан нешеу?

Жауабы: 9⁵

42. Кубикті (шаршыны) үш рет иіргенде кемінде 1 рет «6» цифры түсетін мүмкіндіктер саны қанша?

Жауабы: 6³-5³=91

43. Қабырғалары а) 4; 5; 6; 7 б) 2;5;6;8 сандарына тең болатын әр түрлі неше үшбұрыш болады?

Жауабы: 20

44. 0, 1, 2,..., 9 цифрларының орыналастыруларының нешеуінде 0; 1 цифрлары қатар жазылып, 1; 2 цифрлары қатар келмеген жағдай нешеу.

Нұсқау жауап: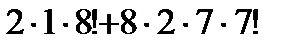

45. Қорап сайын кемінде бір доп болатындай етіп:

а) 10 бірдей допты 4 бірдей қорапқа неше тәсілмен салуға болады?

Нұсқау: Алдымен әр қорапта кемінде бір доп болады деген шартты қананғаттандыратын шара қолдану тура. Соңынан қалған 6 допты 4 қорапқа орналастыру санын доптар мен қораптар бірдей деген есеп шартын ескере отырып табу қажет. Бұл санды «6 санын 4 cанның қосындысына неше тәсілмен қойуға болады?» деген сұраққа жауап беру арқылы табуға болатынына көз жеткіз.

Жауабы: 9 тәсіл

б) 10 әр түрлі допты 4 бірдей қорапқа салу мүмкігдігі нешеу?

Нұсқау: Алдыңғы есептегі әр қадам доптардың әр түрлі болуына байланысты қанша есе артатынын табу қажет. Мәселен: алдыңғы есепте 1 ғана мүмкігдікпен есептелген қораптарға бір бірден салынатын 4 допты таңдау саны 210 -ға тең болатын болады. Қалған 6 доп үшін алдыңғы есептегі 9 жағдайлардың әр қайсысын әр түрлі доптардан таңдау мүмкігдігін есептеп қосып, нәтижені 210-мен көбейтуге тура келеді.

в) 1 0 әр түрлі допты 4 әр түрлі қорапқа салу мүмкігдігі нешеу?

Нұсқау: Алдыңғы есептегі нәтижені пайдаланумен қатар 4 допты әр қорапқа бір бірден орналас-тырғаннан кейін қалған 6 доптың әр қайсысында 4 қораптың қайсысына да түсуге болатын 4 мүміндік болатынын ескеру қажет.

Нұсқау жауап: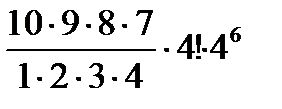

г) 10 бірдей допты 4 әр түрлі қорапқа салу мүмкіндіктері қанша? Жауабы: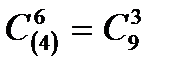

46. Әр түрлі 10 жәшікке бірдей 6 ақ, бірдей 6 қара 12 допты жәшік сайын кемінде 1 доп салынатындай етіп неше әр түрлі тәсілмен орналастыруға болады?

47. теңдеуінің а) Натурал шешімдерінің б) Теріс емес бүтін шешімдерінің санын тап.

Жауабы: a) , б)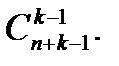

48. Бірдей 15 допты әр түрлі 5 жәшікке 2-ден көп емес бос жәшік болатындай етіп әр түрлі неше тәсілмен салуға болады?

Нұсқау: Бос жәшіктің саны 0, 1, 2 болатан жағдайларды қарастырБір ұлттың 3 адамы қатар отырмайтындай 3 қазақ, 3 орыс, 3 неміс барлығы 9 адамды неше әр түрлі тәсілмен бір қатарға отырғызуға болады?

Ж ауап: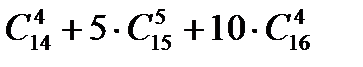

49. Бір ұлттың 3 адамы қатар отырмайтындай 3 қазақ, 3 орыс, 3 неміс барлығы 9 адамды неше әр түрлі тәсілмен бір қатарға отырғызуға болады?

Нұсқау жауап: 9!-3∙3!∙7!+3∙(3!) 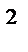∙5! - (3!)

50. а) Алдыңғы есепті бір ұлттың екі адамы қатар отырмайтын жағдайда шеш. б) Дөңгелек үстелді айнала отыратын жағдайда бір ұлттың 2 адамы қатар отырмайтын мүмкіндіктер саны нешеу?

а) Нұсқау жауап: 9!-9∙2!∙8!+27∙(2!) 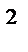∙7!+3!∙7!∙3 - 27∙3!∙ ∙2! ∙6!+ 3!∙ ∙2! ∙6!+ 3∙(3!) 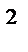∙5!+ 27∙(3!) 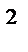- 9∙2! ∙(3!) 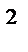∙4!+ (3!) .

51. 4 отбасынан әйел еркектер кездесіп кейбіреулері амандасты және бір үйдің ерлі зайыпты екеуі өзара амандаспайды. Кездескен адамдардың амандасу сандары әр түрлі болған болса кездесуде неше адам болуы мүмкін?

Нұсқау: Келушілер саны 4-тен кем емес. Әр адамның амандасу саны 6- дан артық емес және амандаспаған бір ғана адам болуы мүмкін. Ал амандасулар санының қосындысы жұп сан деген қортындыларға көз жеткізіп, осыларды пайдаланып есепті шеш.

52. Қонақта k ерлі-зайыпты жұптар жиналған. Кездескен кезде кейбір қонаққа келушілер қол алысып амандасты. (Әрине ерлі-зайыпты екі адам бір бірімен амандаспайды.) Осыдан кейін Бөке отырған қауымнан қанша рет қол алып амандасқандары туралы сұрағанда барлық аталған сандар әр түрлі болып шықты. Бөкенің келіншегі қанша рет амандасқанын есептеңіз. Егер: а) k=5, б) k кез келген натурал сан болса

Нұсқау: Бөке өзінен басқа 2k - 1 адамнан сұрағандағы олардың амандасу сандарының жиыны 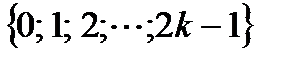болатынын анықта. Амандасу сандары 0 және 2k-2, 1 және 2k-3, 2 және 2k-4 болатын парлар ерлі зайыптылар болуға тиісті екеніне көз жеткіз. Мәселен 2k-2 амандас-қан адам тек 0 санын атаған адаммен ғана амандаспа-ғанда 1 санын атаған адаммен амандасқандықтан 2k-3 рет амандасқан адам 0 және 1 рет амандасқан адаммен амандаспайды д.с к-мен k-2 амандасқан адамдар ерлі зайыптылар болып тек қана k-1 амандасқан адам жеке қалады.

53. (а+1)(в+1)(с+1)(d+1)(e+1)(f+1)(д+1) өрнегінің барлық жақшасын ашып көбейткенде а) Неше қосылғыш пайда болады? б) 3 әріптен тұратын қосылғыш нешеу?

54. Тек көрсетілген бағыт бойынша а) «математика» б) «елорда» в) «құрастырушы» сөздерін неше түрмен оқуға болады?

а) м б) е л о р д а

а а л о р д а

т т т о р д а

е е е е р д а

м м м м м д а

а а а а а а а

т т т т т т т

и и и и и и и и

к к к к к к к к к

а а а а а а а а а а

в) қ ұ р а с т ы

ұ р а с т ы р

р а с т ы р у

а с т р ы у ш

с т ы р у ш ы

Ескерту: Ең үстіңгі немесе үстіңгі жолдың сол шетіндегі әріпт бастап төмен не оңға аттап көшу керек.

55. 1-ден 999999-ға дейінгі сандарды тіркеп жазғанда әр цифр неше рет қайталанады?

56. Бірдей n, әртүрлі n, барлығы 2n доптан n допты неше тәсілмен таңдап алуға болады?

Нұсқау: Бұл жерде таңдалуға тиісті n доптың нешеуі әр түрлі болатынына назар аударылады да қалғаны бірдей доптардан алынады да олар таңдау мүмкіндігіне әсер етпейді. Сондай-ақ әр түрлі доптардың әр қайсысында таңдауға «кіреді», «кірмейді» деген екі мүмкіндік болады.

Жауабы: 2ⁿ

57. 4 х 4 кестенің көздерін әр жолда 4 рең, ал әр бағанда бірдей реңді қатар көз болмайтындай етіп 4 реңмен неше тәсілмен бояуға болады?

Нұсқау: Бірінші жолды 4 реңмен бояу мүмкіндігінің санын тап. Бірінші жолдың бір боялуына есептің шартын орындайтындай екінші жолдың неше мүмкіндігі сәйкес келетінін тап. Жауабы: 17496

1.2. ДИРИХЛЕ ПРИНЦИПІ

Алғаш Неміс математигі Петр Густов Ажен Дирихле (1805-1854жыл) бұл принципті тұжырым-дағандықтан оны Дирихле принципі деп атау қалыптасқан. Бұл принцип қарапайым болғанымен терең логикалық мағынасы бар төменгі тұжырымдармен айқындалады:

1. «n ұяшыққа n+1-ден кем емес қоян орналастырсақ екіден кем емес қоян орналасқан ұяшық табылады»

2. (Кеңейтілген принцип) «nk+1 допты n қорапқа салғанда k+1-ден кем емес дoп салынған қорап табылады»

Жаттығу есептер:

1. Магазинге алманың үш сортынан 25 қорап алма әкелінді кемінде бір сорттан 9-дан кес емес қорап алма болатынын дәлелде,

2. «Зерде» мектебінде 220 оқушы бар. Аттары бірдей әріппен басталатын кемінде 6 оқушы табылатынын дәлелде.

Нұсқау: ь; ъ; й – ден басқа 39 әріпті 39 ұяшық, 220 оқушыны қоян деп ал.

3. Қабырғасы 1 м квадраттың ішінде 51 нүкте берілген. Осы нүктелердің кемінде үшеуі жататын қабырғасы 20 см-ге тең квадрат табылатынын дәлелде.

4. Кез келген 52 бүтін саннан квадраттарының айырмасы 100-ге бөлінетін екі сан табылатынын дәлелде.

Нұсқау: n және 100-n сандарының квадраттарының 100 ге бөлгенде бірдей қалдық беретіндіктен санның квадратын 100-ге бөлгенде 51 әр түрі қалдық шығуы мүмкін

5. 3 х 3 кестесінің көздеріне -1; 0; 1 сандары жазылған. Жолдар, бағандар және екі диоганал бойындағы үштіктердің 8 қосындысынң кемінде екеуінің мәні тең болатынын дәлелде.

Нұсқау: -1; 0; 1 сандарынан жасалатын үштіктердің қосындысының мүмкін мәндерінің жиыны 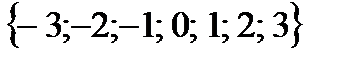болтынына көз жеткіз.

6. 100 адам дөңгелектеп жасалған столға жайғасқан. Олардың жартысынан астамы ерлер болса, бір-біріне қарама-қарсы отырған екі еркек адам табылатынын дәлелде.

Нұсқау: Қарама-қарсы отырған парлар саны 50-ді ұяшық деп алу керек.

7. 1-ден 9-ға дейінгі сандарды үш бөлікке бөлген. Қай бір бөліктегі сандардың көбейтіндісі 72-ден кем емес болатынын дәлелде.

Екі бөліктегі сандардың көбейтіндісі 72-ден кем емес болуы мүмкін бе?

8. 15 оқушыда 100 оқулық болса олардың кемінде екеуінің оқулықтарының саны тең болатынын дәлелде.

Нұсқау: Керісінше барлық оқушының оқулықтарының саны әр түрлі деп көріп, 0 + 1 + 2 +... + 14 = 105 болатынын пайдаланып қорытынды жаса.

9. Кез келген үшеуі бір түзудің бойында жатпайтын 6 нүктені қосатын барлық кесінділерді 2 түске қалай бояса да қабырғалары бірдей түске боялған үшбұрыш табылатынын дәлелде.

10. 1-ден 100-ге дейінгі натурал сандар тізбектей жазылған. Алдымен олардың кез келген 25 саны өшіріледі. Қалған сандардан тағы да 25 санды, қалған 50 санның қосындысы өшірілген 50 санның қосындысына тең болатындай етіп өшіруге бола ма?

11. Төрт тиынның әр қайсысы 100-ден кем емес шәкілдеуік, төртеуі бірігіп 2009 шәкілдеуік жеген. Бірінші тиын ең көп шәкілдеуік жеген де екінші мен үшінші тиындар бірігіп 1265 шәкілдеуік жеген болса тиындардың әр қайсысы неше шәкілдеуіктен жеген.

Нұсқау: Төртінші тиын ең кем дегенде 100 шәкілдеуік жейді 1265 =632 + 633 болатындықтан бірінші тиын 634 тен кем емес шәкілдеуік жеуі қажет екенін ескеріп қорытынды жаса.

12. Кез келген 10 натурал саннан айырмасы 9-ға бөлінетін екі сан табуға болатынын дәлелде

13. Кез келген 31 натурал санның ішінен қандай да екеуінің айырмасы 10-ға бөлінетін 4 сан табылатынын дәлелде.

Нұсқау: 10-ға бөлгендегі қалдықтары тең 4 сан табылатынын дәлелдеп осы сандар есептің шартын қанағаттандыратынына көз жеткізу керек.

14. Күреске 24 балуан қатысты. Әр балуан қарсыластарымен бір рет күреседі. Бәсекенің қай кезеңінде де күрескен сандары тең екі балуан табылатынын дәлелде.

Нұсқау: Қоян – балуандар, ұяшық - олардың күрескен саны. Егер 23 рет күрескен балуан болса онда күреспеген балуан жоқ та күреспеген балуан болса 23 күрескен балуан болмайтыны ұяшықтың санын 23-тен азайтуға мүмкіндік беретінін ескер.

15. Кез келген 5 натурал саннан квадраттарының айырмасы 7-ге бөлінетіндей екі сан табылады деген қортынды жасауға бола ма?

Нұсқау: Натурал санның квадратын 7-ге бөлгенде 0; 1; 2; 4; қалдық қалатынын ескер.

16. Кез келген жеті бүтін саннан қосындысы 3-ке бөлінетін үш сан табылатынын дәлелде.

Нұсқау: a ≡ 0; 1; 2(mod3) болатынын және 3-ке бөлгендегі қалдықтары тең үш санның қосындысы 3-ке бөлінетінін ескер.

17. 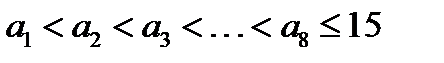шартын қанағаттандыратын 8 натурал сан берілген. Барлық мүмкін 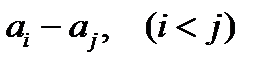айырмаларының кемінде үшеуі өзара тең болатынын дәлелде.

Нұсқау: Мәні 14-ке тең айырма бірден артық емес, ал есептің шартындағы айырмалардың саны нешеу болаты-нын анықта.

18. Кез келген натурал сан үшін оған бөлінетін 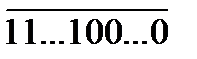түріндегі сан табылатынын дәлелде.

Нұсқау: 1, 11, 111, ..., 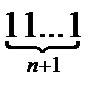деген n+1 санды қоян ретінде, оларды n-ге бөлгенде шығатын қалдықтарды ұяшық ретінде алып қорытынды жаса.

19. Қорапта 25 ақ, 25 қара, 20 көк, 10 қызыл доп бар. а) Қандай бір өңнен 10 доп, б) 10 ақ доп алған болу үшін қараңғыда қораптан неше доп алу қажет?

20. Сыныпта 30 оқушы бар. Диктант жазғанда Айдын 13 қате, қалғандары одан аз қате жіберген. Жіберген қателерінің саны бірдей үш оқушы табылатынын дәлелде.

21. Кез келген 65 натурал саннан қосындысы 9-ға бөліне-тін 9 сан табылатынын дәлелде.

Нұсқау: 9-ға бөлгенде бірдей қалдық беретін 9 сан және 9-ға бөлгенде әр түрлі қалдық беретін 9 санның қосындысының 9-ға бөлінетінін анықта.

22. Қабырғасы 5 см квадраттың ішінде 127 нүкте берілген. Бұлардан радиусы 1 см дөңгелектің ішінде жататын 8 нүкте табылатынын дәлелде.

Нұсқау: Берілген квадратты бірдей квадраттарға бөлу арқылы шешу жолын қарастыру

23. Бір тұрғын үйде 123 адам өмір сүреді. Олардың жастарының қосындысы 3813. Бұлардан жастарының қосындысы 3100-ден кем емес 100 адам таңдап алуға бола ма?

24. Жазықтықта қандай да екеуі параллель болмайтын 7 түзу берілген. Бұлардан арасындағы бұрышы 26°-тан кіші болатын екі түзу таңдап алуға болатынын дәлелде. 26°-ты 25°-пен алмастырса қорытынды ақиқат бола ала ма?

25. 21 бала 200 шәкілдеуікті барлық баланың алған шәкілдеуігінің саны әр түрлі болатындай етіп бөліп ала ала ма? (0 шәкілдеуік алған бала болуға болады.)

26. Ұзындықтары 10 см-ден артық, 1 м-ден кем 7 кесінді берілген. Бұлардан үшбұрыш құрастыруға болатын үш кесінді табылатынын дәлелде.

27. Кез келген n+2 натурал саннан не қосындысы не айырмасы 2n-ге бөлінетін екі сан таңдап алуға болатынын дәлелде.

Нұсқау: Санды 2n-ге бөлгенде шығатын қалдықтарды 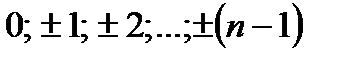түрінде қарастырайық. 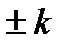қалдық беретін сандарды k-інші ұяшыққа орналастырамыз. Немесе 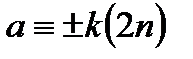болса а саны k-інші ұяшыққа салынуы керек.

28. Екі таңбалы әр түрлі 10 натурал саннан топтардағы сандардың қосындысы тең болатындай екі топ таңдауға болатынын дәлелде.

Нұсқау: 10 элементті жиынның құр емес ішкі жиындарының саны 1023, қандай да ішкі жиынның элементтерінің қосындысы 990-нан артпайтынын айқындап, пайдалан.

29. Қабырғасы 1-ге тең квадратта 64 нүкте берілген. Осы нүктелердің қай бір үшеуін радиусы 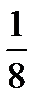-ге тең шеңберге сиғызуға болатынын дәлелде.

Нұсқау: Центрі берілген нүктелерде радиусы 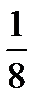-ге тең дөңгелектерді алып көрейік. Олардың аудандарының қосындысы 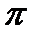және бұл дөңгелектердің бәрі берілген квадраттарды сыртынан 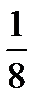қашықтықта қоршайтын 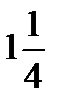қабырғалы квадратқа сияды. Дирикле принципінің үздіксіздік қасиетін пайдаланып ортақ нүктесі болатын кемінде үш шеңбер табылатынына көз жеткіз. Олардың центрлері болатын үш нүктені алып көр.

30. Кез келген n бүтін сан үшін не олардың қайсы біреуі не қай бір екеунің айырмасы n-ге бөлінетінін дәлелде.

31. 2n-нен артпайтын әр түрлі n+1 натурал саннан біреуі келесі екеуінің айырмасына тең болатын үш сан таңдап алуға болатынын дәлелде.

Нұсқау: Сандарды 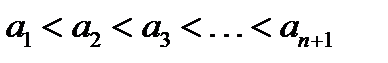деп белгілеп, 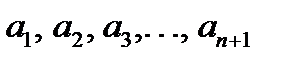-лермен қатар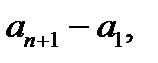 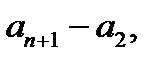..., 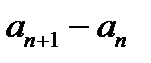айырмаларын алып, қортынды жаса.

32. Кез келген n-натурал сандардан қосындысы n-ге бөлінетін бірнеше сан табылатынын дәлелде.

Нұсқау: 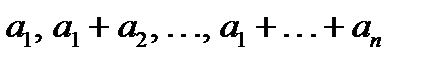қосындылары мен олардың екі екіден алғандағы айырмаларын қарастыр.

33. Дөңес 9 бұрыш диагоналдарынан арасындағы бұрышы 7 градустан кем болатын екі диагонал табылатынын дәлелде.

34. Қабырғасы 1-ге тең дұрыс үшбұрыштың ішінде 5 нүкте берілген болса олардың қай бір екеуінің ара қашықтығы 0,5-тен кем болатынын дәлелде.

Нұсқау: Үшбұрыштың орта сызықтарын жүргіз.

35. Жазықтықтағы берілген 25 нүктенің қандай да үшеуін алғанда кемінде екеуінің ара қашықтығын 1-ден кіші болса олардың 13- тен кем емесін 1 радиусты дөңгелекке сыйғызуға болатынын дәлелде.

Нұсқау: Ең алыс орналасқан екі нүктені алып центрі сол нүктелерде жататын радиусы 1-ге тең дөңгелектерді қарастыр.

Дата добавления: 2014-12-16